Ouvindo a gravidade
Talvez se perguntássemos para uma pessoa se os objetos caem com velocidade constante ou acelerada, a pergunta poderia gerar um pouco de dúvida. Você então poderia mostrar a ela qual a resposta fazendo um experimento simples de soltar um objeto em direção ao solo.
O grande problema deste experimento é que os nossos olhos não conseguem acompanhar o movimento e é muito difícil chegar a uma conclusão clara apenas com os nossos sentidos visuais. Você talvez então proporia que, com as tecnologias disponíveis no mundo atual, filmássemos o movimento para depois analisar o filme, quadro a quadro, e determinar se o movimento é acelerado ou não. Mas imagine isso a quatro séculos atrás! Como saber se os objetos caem na superfície da Terra acelerados ou não?
Vamos propor uma alternativa de experimento, utilizando a nossa audição. Já pensou em conseguir “ouvir” a aceleração da gravidade?
Experimento
Com cinco parafusos (porcas ou outros objetos semelhantes), monte dois arranjos amarrando-as em um barbante. No primeiro arranjo, amarre as porcas, separando-as em distâncias iguais de 30 cm. No outro arranjo, amarre-as também mas com distâncias entre elas de 10 , 30, 50 e 70 cm. Aqui utilizamos parafusos que estavam a disposição. Alinhe cada arranjo na vertical sobre um anteparo e solte-o. O anteparo pode ser uma caixa plástica ou de madeira para receber os impactos e amplificar o som produzido pelo impacto dos parafusos. Grave o som das colisões dos parafusos com o anteparo para cada arranjo individualmente (você pode usar aplicativos para o celular como este aqui). Você acabou de realizar um experimento científico e, com ele, coletou dados experimentais na forma de um gráfico da intensidade sonora em função do tempo! A partir do gráfico, você pode determinar o intervalo de tempo entre as colisões.
Modelo
Agora vamos propor um modelo para explicar o fenômeno. Vamos supor que o movimento dos parafusos ao cair é acelerado, ou seja, suas velocidades mudam com o tempo.
A posição \(S\) de um objeto em função do tempo \(t\), caindo com uma aceleração constante \(g\) é dado por
\[S=S_0+V_0 t - \frac{1}{2}gt^{2},\]
onde \(S_0\) é a posição do objeto no momento da largada e \(V_0\) é a velocidade que ele é solto. Assumiremos que largamos o objeto, ou seja, \(V_0=0\).
O tempo de queda do objeto \(i\), ou seja, o tempo que leva para percorrer uma distância \(\Delta S_i \equiv S_{0i}-S\) é
\[t_i=\sqrt{\frac{2 \Delta S_i}{g}}.\]
Escolhendo a posição do anteparo como sendo \(S=0\) então
\[t_i=\sqrt{\frac{2 S_{0i}}{g}}.\]
O tempo entre a colisão do parafuso \(i\) e \(i+1\), \(\Delta t_i\), será
\[\Delta t_i=\sqrt{\frac{2 S_{0i+1}}{g}} -\sqrt{\frac{2 S_{0i}}{g}}= \sqrt{\frac{2}{g}}(\sqrt{S_{0i+1}}-\sqrt{S_{0i}}).\]
Para o arranjo com espaçamento iguais valendo \(d\), temos que \(S_{0i+1}-S_{0i} = d\) ( \(S_{04}-S_{03}=d, \; S_{03}-S_{02}=d, \; S_{02}-S_{01}=d\) ) e assim
\[\Delta t_i= \sqrt{ \frac{2}{g} } (\sqrt{S_{0i}+d} - \sqrt{S_{0i}} ).\]
Na equação acima, vemos que \(\Delta t_i\) será diferente para cada parafuso pois ele depende da posição \(S_{0i}\) de cada parafuso.
Para o arranjo com espaçamento diferentes, temos que \(S_{0i}=(i-1)^2D\) e \(S_{0i+1}=(i)^2D\) (Verifique!). \(D\) é um fator de escala que no nosso caso vale 10 cm. Assim
\[\Delta t_i= \sqrt{ \frac{2}{g} } (\sqrt{S_{0i+1}}-\sqrt{S_{0i}}) = \sqrt{ \frac{2}{g} }( i\sqrt{D}-(i-1)\sqrt{D}),\]
ou ainda,
\[\Delta t_i= \sqrt{\frac{2D}{g}}.\]
Na equação acima, vemos que \(\Delta t_i\) não depende de \(i\), ou seja, é o mesmo valor para todos os parafusos!
Ao compararmos os gráficos da intensidade do som em função do tempo para os dois arranjos poderemos verificar se o nosso modelo está correto e se ele pode ser usado para explicar o que está acontecendo.

Quando temos espaçamentos iguais entre os parafusos (primeiro arranjo), vocês iriam ouvir as colisões em intervalos aproximadamente iguais, se a queda não fosse acelerada. No entanto, isso não é o que se observa analisando as gravações dos áudios. O que se percebe é que as colisões dos últimos parafusos com o anteparo produzem sons em intervalos menores de tempo que os produzidos pelos primeiros parafusos.
Quando temos espaçamentos diferentes (segundo arranjo), o som produzido entre colisões sucessivas ocorrem em intervalos de tempo aproximadamente iguais pois cada parafuso leva um tempo maior para cair devido ao seu espaçamento distinto.
O que vemos, ou melhor, o que ouvimos, é um movimento acelerado!
Primeiro áudio:
Segundo áudio:
Está correto dizer que o segundo áudio corresponde à configuração de parafusos com espaçamentos iguais? Confira a resposta aqui.
Foi difícil perceber a diferença entre os dois áudios, não foi ?
Então “veja” agora o som de cada um deles no gráfico abaixo, o qual mostra a intensidade do som em função do tempo para cada caso. O tempo total da gravação foi de aproximadamente 0.65 s.
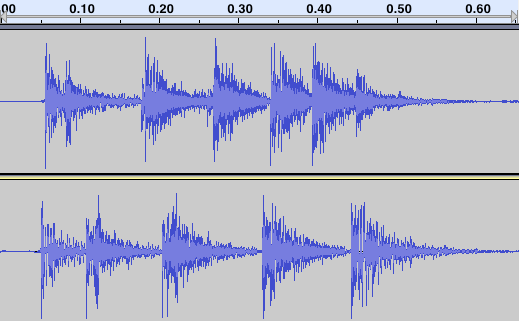
Para os curiosos
Para aqueles que quiserem saber um pouco mais sobre a história de gravidade e os métodos utilizados para determinar a aceleração da gravidade, vejam “A História da Gravidade” e “Determinando a aceleração gravitacional”.