from IPython.display import clear_output
!sudo apt update
!sudo apt install libcairo2-dev ffmpeg \
texlive texlive-latex-extra texlive-fonts-extra \
texlive-latex-recommended texlive-science \
tipa libpango1.0-dev
!pip install manim
!pip install IPython --upgrade
clear_output()Manual do Manim
Projeto PIBIC: Desenvolvimento de animações para o ensino de matemática usando o Manim
CNPq: 0220036212472856
Autor: Eric Satoshi Suzuki Kishimoto
Orientador: Prof. Vitor Rafael Coluci (Faculdade de Tecnologia/UNICAMP)
#
- Introdução
Este manual aborda conceitos de programação em Python voltada para o uso da biblioteca Manim. Nesta seção introduziremos a biblioteca Manim e mostraremos como instalá-la no Google Colab.
##1.1 O que é o Manim?
Manim é uma biblioteca da linguagem de programação Python, criada por Grant Sanderson, idealizador do canal 3blue1brown. Neste canal, Sanderson disponibiliza vídeos de animações matemáticas utilizando essa biblioteca.
##1.2 Instalação do Manim no Colab

Para tornar o uso do Manim mais simples, usaremos o Google Colab, uma plataforma gratuita para criar códigos em Python. Nesta plataforma, cada arquivo é chamado de notebook. Um notebook é dividido em células e pode conter tanto textos como códigos.
Para instalar o Manim no Google Colab, basta executar o seguinte código, pressione Shift + Enter ou Ctrl + Enter.
Obs: O código a seguir pode demorar um tempo para rodar.
Para que o Manim funcione, é necessário reiniciar o ambiente de execução. Para isso, acesse o menu Ambiente de execução → Reiniciar ambiente de execução.

Para verificar se tudo está funcionando, execute o seguinte código.
from manim import *Manim Community v0.11.0
Caso apareça a mensagem
Manim Community v0.11.0ou algo parecido, o Manim foi instalado com sucesso.
Caso apareça uma mensagem de erro, o Manim não foi instalado corretamente. Tente reexecutar as instruções anteriores.
##1.3 Primeira animação
Agora que instalamos o Manim no Google Colab, podemos começar a criar animações. Para dar um exemplo das animações que a biblioteca pode fazer, execute o seguinte código.
%%manim -qm -v WARNING PrimeiraAnimacao
class PrimeiraAnimacao(Scene):
def construct(self):
quadrado = Square()
circulo = Circle()
self.play(Write(quadrado))
self.play(ReplacementTransform(quadrado, circulo))A primeira linha de código (%%manim -qm -v WARNING PrimeiraAnimacao) possui os comandos para renderizar a animação PrimeiraAnimacao. Futuramente, veremos como funciona a linha de comando com Manim mas, basicamente para o exemplo apresentado, pedimos para que a animação seja renderizada em qualidade média limpando toda a saída do terminal (opção -qm).
#
- Introdução ao Python

Antes de começar a criar as animações com o Manim, iremos abordar a programação em Python, uma linguagem de programação usada em diversas áreas como data science, machine learning, desenvolvimento web, entre outros. Neste manual, abordaremos como usar essa linguagem de programaçao para criar animações com o Manim. Se você já está familiarizado com o Python, você pode avançar para a seção onde descrevemos o Manim, em Introdução ao Manim.
##2.1 Conceitos básicos
Começaremos escrevendo nosso primeiro código em Python.
print('Hello World')O código acima imprime na tela a frase “Hello World”. Ele é o primeiro programa de muitos programadores e serve para verificar se tudo está funcionando corretamente. Entretanto, ele não faz muita coisa. Por isso, vamos abordar os conceitos básicos que nos permitirão fazer muitas coisas legais.
###2.1.1 Variáveis
O primeiro conceito que abordaremos é o de variáveis. Imagine elas como caixas que guardam dados como textos, números, entre outros. Para criar uma variável em Python, escrevemos seu nome e atribuímos um valor para ela, como mostrado no exemplo a seguir.
pi = 3.14
texto = 'pi'
print(pi)
print(texto)Existem algumas regras para nomear as variáveis:
- Devem começar com uma letra ou underline (_).
- Não podem iniciar com números.
- O Python diferencia letras maiúsculas e minúsculas.
- Não devem ter caracteres especiais como acentos e pontuações.
2.1.2 Tipos de dados
Cada variável possui um tipo de dado, podendo ser números, textos, entre outros.
Os tipos mais básicos em Python, também conhecidos como primitivos, são:
str: também conhecida com string. É uma cadeia de caracteres, ou seja, texto. Precisa estar entre aspas simples ou duplas.int: números inteiros.float: números de ponto flutuante, ou seja, números reais.bool: variáveis que podem ter 2 valoresTrueeFalse.
numero_real = 2.71
numero_inteiro = 1
texto = 'Variável do tipo texto'
verdadeiro = True
print(numero_real)
print(numero_inteiro)
print(texto)
print(verdadeiro)2.1.3 Operadores aritméticos
Além de armazenar dados, as variáveis podem ser utilizadas para realizar operações. Entre variáveis dos tipos int e float, podemos realizar operações matemáticas como: * Adição (+) * Subtração (-) * Multiplicação () Divisão (/) * Módulo (%): resto da divisão * Exponenciação (**)
pi = 3.14
e = 2.71
add = pi + e
sub = pi - e
mult = pi * e
div = pi / e
mod = pi % e
exp = pi ** e
print('Adição: ', add)
print('Subtração: ', sub)
print('Multiplicação: ', mult)
print('Divisão: ', div)
print('Módulo: ', mod)
print('Exponenciação: ', exp)2.1.4 Operações com strings
Operações podem ser aplicadas não somente a números, mas também a textos. Em Python, temos as segiuntes operações: * Concatenação: adição de 2 ou mais strings (+) * Multiplicação por inteiro: resultando na repetição da strings (*)
Também temos a f-string que torna a concatenação de strings com variáveis mais simples. Colocamos um f antes da string.
string1 = 'Hello'
string2 = 'World'
print('Concatenação: ', string1 + string2)
print('Multiplicação por inteiro: ', 3 * string1)
print(f'f-string: {string1} {string2}')2.1.5 Operaçõe booleanas
Temos também as operações booleanas. Basicamente, utilizamos operações booleanas para realizar comparações. Utilizamos comparações com os seguintes operadores. * ==: compara se dois valores são iguais. * !=: compara se dois valores são diferentes. * >: compara se um valor é maior que o outro. * >=: compara se um valor é maior ou igual ao outro. * <: compara se um valor é menor que o outro. * <=: compara se um valor é menor ou igual ao outro.
Todas essas comparações podem resultar em apenas um dos resultados: True ou False.
valor = 5
print(valor == 6)
print(valor != 5)
print(valor > 6)
print(valor >= 6)
print(valor < 6)
print(valor <= 6)Obs: Veremos na seção Estrutura de controle como usamos esssas expresões.
Além dessas comparações, podemos utilizar os operadores and, or e not para combinar as comparações ou tipos booleanos.
and: resulta verdadeiro apenas se as 2 comparações forem verdadeiras. Caso contrário, resulta falso.or: resulta verdadeiro se qualquer uma das 2 comparações forem verdadeiras. Se ambas forem falsas, resulta em falso.not: inverte o valor da expressão, ou seja, resulta emTruese forFalsee resulta emFalsese forTrue.
print('True and True: ', True and True)
print('True and False: ', True and False)
print('False and True: ', False and True)
print('False and False: ', False and False)
print('True or True: ', True or True)
print('True or False: ', True or False)
print('False or True: ', False or True)
print('False or False: ', False or False)
print('not True: ', not True)
print('not False: ', not False)2.1.6 Operações de atribuição
Até agora, utilizamos um símbolo que não foi explicado, o =. Ele não funciona como o sinal de igual da matemática. Ele é um operador de atribuição, ou seja, usado para atribuir valor às variáveis. Por exemplo, no código a seguir:
var = 3podemos interpretar que var recebe o valor 3. Há outras formas de realizar a atribuição de variáveis, por exemplo:
- Adição:
var = var + 2→var += 2 - Subtração:
var = var - 2→var -= 2 - Multiplicação:
var = var * 2→var *= 2 - Divisão:
var = var / 2→var /= 2 - Exponenciação:
var = var ** 2→var **= 2
var = 3
print('Variável antes da atribuição: ', var)
var += 2
print('Adição: ', var)
var -= 2
print('Subtração: ', var)
var *= 2
print('Multiplicação: ', var)
var /= 2
print('Divisão: ', var)
var **= 2
print('Exponenciação: ', var)2.1.7 Comentários
Às vezes, o código pode ficar muito grande e complexo e seria interessante ter anotações sobre o que cada parte do código faz. Comentários não são executados, o que permite incluir anotações dentro do código. Para isso, usamos os comentários. Usamos o # Comantário para comentários de linha única e ''' comentário ''' ou """ comentário """ para comentário de múltiplas linhas.
# Linha comentada
print('Linha não comantada')
'''
Linhas
Comentadas
'''
print('Linha não comentada')2.1.8 Variáveis no Manim
Para começarmos a ver a conexão entre os conceitos vistos neste tópico e as animações produzidas pelo Manim, vamos criar uma pequena animação. Por exemplo, uma animação que armazena duas fórmulas f1 e f2 (armazenadas como variáveis), escreve f1 na tela e depois a transforma f1 em f2.
%%manim -qm -v WARNING Variaveis
class Variaveis(Scene):
def construct(self):
f1 = MathTex('y = ax + b').scale(2)
f2 = MathTex('y = 2x + 1').scale(2)
self.play(Write(f1))
self.play(TransformMatchingTex(f1, f2))
self.wait()2.2 Mais tipos
Além dos tipos primitivos, existem outros tipos no Python que iremos abordá-los nesta seção.
###2.2.1 Listas
Às vezes, queremos armazenar diversos valores em uma única variável. Para isso, usamos listas. Para criá-las, usamos colchetes ([]) e inserimos os valores separados por vírgulas ,. Chamamos cada valor da lista de elemento e podemos acessá-los através de índices (números inteiros começando do 0).
Podemos visulizar uma lista através da figura abaixo. Ela possui diversos elementos [3.14, 2.72, 0, 1, []] e podem ser acessados pelos índices 0 à 4 ou de trás para frente de -1 à -5.

numeros_naturais = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print('Lista: ', numeros_naturais)
print('Elemento 1:', numeros_naturais[0])Obs: Podemos ter listas dentro de listas como matrizes. Para acessar seus elementos, basta adicionar colchetes. Exemplo:
matriz[0][0]
Além dessas operações, também podemos realizar algumas operações de conjuntos matemáticos:
in: Verifica se um elemento pertence ao conjunto.not in: Verifica se um elemento não está no conjunto.+: Soma 2 listas resultando em outra lista.*: Repete a lista.len: Retorna o número de elementos da lista
numeros_racionais = [0.1, 0.2, 0.3, 0.4]
numeros_irracionais = [3.14, 2.72]
print(0.1 in numeros_racionais)
print(0.5 not in numeros_racionais)
print(numeros_irracionais + numeros_racionais)
print(3 * numeros_irracionais)
print(len(numeros_irracionais))2.2.2 Listas fatiadas
Vimos como acessar um elemento de uma lista, mas como acessar um intervalo? Para isso, usamos listas fatiadas. Inserimos um intervalo dentro do colchetes, separando o intervalo por dois pontos : como mostrado no exemplo a seguir:
numeros_primos = [2, 3, 4, 7, 11]
print(numeros_primos[0:3])Acima, o intervalo começa em 0 e termina em 3-1=2. Existem outras formas de fatiar uma lista.
- Adicionando um terceiro número: são os passos com que a lista será fatiada. Se o terceiro número for 2, a lista pegara de 2 em 2 elementos.
- Omitindo o segundo número: percorre até o final da lista.
- Omitindo o primeiro número: percorre desde o começo da lista.
numeros_inteiros = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print('Adicionar passos: ', numeros_inteiros[0:10:2])
print('Omitindo o segundo número', numeros_inteiros[5:])
print('Omitindo o primeiro número', numeros_inteiros[:5])2.2.3 Dicionários
Nas listas, acessávamos seus elementos através de números inteiros. Nos dicionários podemos usar além de inteiros, floats e strings. Para declarar um dicionário, basta usar chaves ({}).
numeros_irracionais = {
'pi': 3.14,
'e': 2.72
}
print(numeros_irracionais)
print(numeros_irracionais['pi'])Como podemos observar, dicionários são conjuntos de chave : valor. Podemos enxergar um dicionário com a figura a seguir. Nela, os valores à esquerda são as chaves e os valores à direita são os valores.

Podemos acessar essas chaves e valores com os métodos keys e values. Iremos explicar o que são métodos na seção de Programação Orientada a Objetos. Por agora, podemos considerar que são códigos que realizam tarefas sem sabermos sua implementação.
print(numeros_irracionais.keys())
print(numeros_irracionais.values())2.2.4 Tuplas
Também temos o tipo de dado tupla. Ela funciona da mesma forma que a lista. A única dferença é que não podemos mudar seus elementos. Declaramos uma tupla com parênteses (). Outra opção de declaração é a de separar os items entre vírgulas ,.
conjunto_reais = (3.14, 2.71, 0, 1, 2, 3)
conjunto_inteiros = 1, 2, 3, 4, 5, 6
print(conjunto_reais)
print(conjunto_inteiros)
print(conjunto_inteiros[4:])
print(conjunto_inteiros[:4])
print(conjunto_inteiros[4])
print(conjunto_inteiros[:])Como podemos perceber, todas operações que realizamos com listas podem ser realizadas com tuplas. Veremos mais a frente algumas coisas que são feitas apenas com tuplas.
###2.2.5 Listas e Tuplas no Manim
Vamos ver um pouco como utilizar listas e tuplas no Manim. É muito comum mover objetos gráficos no Manim. Para isso, utilizamos listas para representar as coordenadas desses objetos.
%%manim -qm -v WARNING ListasTuplas
class ListasTuplas(Scene):
def construct(self):
pos1 = [0, 2, 0]
pos2 = [0, -2, 0]
quad = Square()
self.play(Write(quad))
self.play(quad.animate.move_to(pos1))
self.play(quad.animate.move_to(pos2))2.3 Estruturas de controle
Agora que vimos os tipos de dados, precisamos entender como manipulá-los. Para isso, usaremos as estruturas de controle. Abordaremos aqui as estruturas if, else, elif, while e for.
2.3.1 if else
A primeira estrutura de controle que abordaremos será o if. Basicamente o que ele faz é verificar se uma condição é verdadeira. Se for, o código dentro é executado. Se não for, o código não é executado.
num = 2
if num % 2 == 0:
print(f'{num} é par')Acima, verificamos se a variável num é par, ou seja, se o resto da divisão por 2 é 0. Se for, o código imprime “2 é par”.
Obs: tabulações são usadas para colocar um código dentro de uma estrutura
Agora que aprendemos o se (if), precisamos do se não (else). Basicamente, se a condição no if for falsa, ela é redirecionada para o else.
num = 3
if num % 2 == 0:
print(f'{num} é par')
else:
print(f'{num} é impar')De forma gráfica, podemos ver essa estrutura da seguinte forma.

2.3.2 elif
Uma estrutura complementar ao if else é o elif. Basicamente, em vez de apenas 2 condições, podemos encadiar várias delas.

num = 5
if num < 5:
print(f'{num} é menor que 5')
elif num == 5:
print(f'{num} é 5')
elif num > 5:
print(f'{num} é maior que 5')
else:
print(f'{num} não é um número')2.3.3 while
Existem situações onde queremos que o mesmo trecho de código se repita diversas vezes. Para isso, usamos o laço (loop) while. Por ele, passamos uma comparação que executa um código até que a condição seja falsa.

vezes = 0
while vezes < 5:
print(f'{vezes} é menor que 5')
vezes += 1Obs: Tome cuidado apenas quando a expressão for sempre verdadeira. Isso é o que chamamos de loop infinito. Nestes casos, ela será executada até que aconteça um erro. Esse erro acontece pois a memória - que é onde os dados do computador são armazenados - fica toda ocupada. Não abordaremos com profundidade como a memória do computador funciona, mas ela não é ilimitada. Entretanto, não precisamos nos preocupar tanto com isso. Basta evitarmos loop infinitos.
###Obs: O loop
whilenão é tão utilizado pois a estrutura a seguir que veremos (for) nos permite fazer a mesma coisa de forma mais fácil. Porém, é bom saber como owhilefunciona.
3.3.4 break
Se quisermos sair da estrutura while mesmo que a condição ainda seja verdadeira, usamos a expressão break.
contador = 0
while contador < 5:
print(f'{contador} é menor que 5')
if contador == 3:
break
contador += 12.3.5 for
Outra estrutura que abordaremos é o loop for. Nele, iteramos os elementos de uma lista. Não está escrito errado, iterar significa passar por cada um dos elementos de uma lista ou estruturas com diversos elementos. Usamos o for junto com o in.
numeros_inteiros = [1, 2, 3, 4, 5]
for numero in numeros_inteiros:
print(numero)###Obs: Ambos
whileeforsão estruturas de repetição, ou seja, eles repetem a parte do código diversas vezes. Normalmente oforé mais utilizado por por ser mais simples de escrever. Nowhile, precisamos criar uma variável para contar quantas vezes e ainda precisamos incrementá-la. Nofor, precisamos apenas de uma lista ou do range que veremos no próximo tópico.
2.3.6 range
Além de usar listas, podemos usar o range para iterar elementos. Ele basicamente cria uma sequencia de números.
for i in range(5):
print(i)Também podemos adicionar outros números para indicar o começo, o fim e o passo, como fazemos nas listas fatiadas.
for i in range(3, 9, 2):
print(i)2.3.7 Compreensões de listas
Agora que sabemos como usar o loop for, vamos ver uma forma mais simples de criar uma lista. Podemos criá-la com um loop for de forma simples, como mostrado no exemplo abaixo.
lista = [item for item in range(9)]
print(lista)2.3.8 Operador ternário
Podemos usar a estrutura do if else em uma só linha. Usamos o operador ternário para isso.
num = 5
if num > 10:
print(f'{num} é maior que 10')
else:
print(f'{num} não é maior que 10')
print(f'{num} é maior que 10') if num > 10 else print(f'{num} não é maior que 10')2.4 Funções
Até agora, vimos tudo que precisamos para criar nossos próprios programas. Entretanto, ter diversas linhas de código iguais é ineficiente. Para isso, utilizaremos funções.
###2.4.1 Reuso de código
Muitas vezes, repetimos o mesmo código diversas vezes. Por exemplo, quando queremos fazer a média de 3 listas.
lista1 = [3.14, 2.72, 9.8]
somatorio1 = 0
for numero in lista1:
somatorio1 += numero
print(somatorio1)
lista2 = [2, 4, 6, 8]
somatorio2 = 0
for numero in lista2:
somatorio2 += numero
print(somatorio2)
lista3 = [1, 3, 5, 7, 9]
somatorio3 = 0
for numero in lista3:
somatorio3 += numero
print(somatorio3)Estamos repetindo o mesmo código diversas vezes. Para evitar isso, usamos funções.
def somatorio(lista):
somatorio = 0
for numero in lista:
somatorio += numero
return somatorio
print(somatorio(lista1))
print(somatorio(lista2))
print(somatorio(lista3))Como podemos observar, a quantidade de linhas de código foi bastante reduzida. Uma função é declarada apenas uma vez e pode ser chamada quantas vezes forem necessárias, diminuindo consideravelmente a quantidade de linhas de código.
Obs: a função acima possui grande parte dos elementos de uma função que veremos a seguir.
Em programação, o uso de funções é muito importante. Nos exemplos desse manual, são abordados exemplos simples com poucas linhas de código. Mas, em códigos como as das animações do canal 3b1b, podem haver centenas ou milhares de linhas de código. Se não fossem usadas funções, haveria muito mais linhas de código e possivelmente estaria muito mais desorganizado.
###2.4.2 O que são funções?
Até agora discutimos qual a importância das funções e do reuso do código, mas o que exatamente são funções? São pedaços de código que podem ser reutilizados pelo programa. Também podemos utilizar a definição matemática que é algo que recebe entradas e que fornece saídas. Já utilizamos algumas funções neste manual como o print e o range.
print('Isso é uma função')
range(3, 10)Essas funções são pré-definidas pelo Python, mas podemos criar nossas próprias funções usando a palavra-chave def.
def funcao():
print('Isso é uma função')
funcao()Podemos fazer 2 coisas com uma função: definí-la e chamá-la. Acima, usamos o def para definí-la e a chamamos digitando seu nome seguido de parenteses ().
2.4.3 Escopo
Escopo é um conceito que deixa muitas pessoas confusas quando estão vendo programação pela primeira vez. Mas podemos definí-lo como o lugar onde variáveis ou funções estão no código. Podemos ter um escopo mais “aberto” ou um mais “fechado”.
def escopo_fechado():
var_interna = 1
var_externa = 3
print(var_externa)
print(var_interna)Ao executarmos o código acima, teremos um erro dizendo que a variável var_interna não está definida. Mas definimos ela dentro da função. Isso acontece porque definimos ela dentro de um escopo mais fechado e o escopo mais aberto não consegue enxergar variáveis.
Obs: não se assuste com erros, eles aparecerão com muita frequência enquanto você criar os códigos das animações.
Para simplificar as coisas podemos definir que:
Escopo mais aberto não consegue enxergar variáveis ou funções em escopos mais fechados.
###Obs: quando uma função termina, todas suas variáveis internas são destruídas.
2.4.4 Argumentos
Anteriormente indicamos que funções podem receber entradas. Para isso, informamos essas entradas dentro de parenteses.
def media(numeros):
media = 0
for numero in numeros:
media += numero
print(media/len(numeros))
notas = [7, 5, 8, 10, 3]
media(notas)###Obs: Argumentos são definidos como as entradas quando declaramos a função. Já os parâmetros são os valores que passamos para função. Essa definição não é obrigatória e podemos usar apenas argumentos ou parâmetros para essas duas definições.
2.4.5 Parâmetros Padrão
Se quisermos usar uma função sem precisar ficar toda hora passando parâmetros, podemos criar parâmetros padrão que substituirão os valores dos argumentos se os parâmetros não forem passados.
def parametros(a, b, c=1, d=2):
print(a, b, c, d)
parametros(3, 4)###Obs: os parâmetros padrão devem ser os últimos da definição da função. Caso contrário, ocorrerá um erro.
2.4.6 Parâmetros nomeados
Em funções com muitos parâmetros, podemos ficar confusos quanto à ordem dos argumentos. Para simplificar o processo, usamos parâmetros nomeados na chamada da função e, com isso, podemos passar o nome do parâmetro que queremos.
def parametros(a, b, c, d):
print(a, b, c, d)
parametros(1, 2, c=3, d=4)Obs: Parâmetros não nomeados são chamados de parâmetros posicionais, uma vez que dependem da posição onde são passados.
###Obs: Parâmetros posicionais devem ser passados antes dos nomeados.
2.4.7 Retorno
Até agora, apenas passamos as entradas para a função e as usamos dentro da função. Isso não é recomendado pois precisamos usar os resultados calculados dentro da função fora dela. Para isso, usamos a palavra-chave return, ou seja, a saída da função.
def soma(a, b):
return a + b
resultado = soma(1, 2)
print(resultado)
print(soma(3, 4))
print(soma)Obs: Temos que tomar cuidado com o tipo de retorno da função. Se passarmos esse retorno como parâmetro de outra função, temos que verificar qual o tipo que estamos passando.
###Obs: Precisamos colocar o parênteses quando chamamos a função. Se não o fizermos, ela retornará um objeto
function. Veremos mais sobre objetos na seção Programação orientada a objetos.
2.4.8 Desempacotamento de listas e tuplas
Esse tópico é tratado como avançado para quem aprende a programar por ser uma ferramenta única do Python. Entretanto, é um conceito muito importante para a parte de funções do Python. Esse conceito permite diversas coisas, entre elas:
- Retornar vários valores (Em outras linguagens de programação, seria necessário o uso de arrays ou listas)
def retornar_irracionais():
return 3.14, 2.72
print(retornar_irracionais())- Atribuir mais de um valor à mais de uma variável (normalmente fazemos isso para diminuir a quantidade de linhas de código)
valor1, valor2 = 3.14, 2.72
print(valor1)
print(valor2)- Passar diversos argumentos para uma função (Isso é um recurso extremamente utilizado no Manim e em outras bibliotecas do Python)
def somatorio(*nums):
soma = 0
for num in nums:
soma += num
return soma
print(somatorio(1, 2, 3))
2.4.9 lambda
Uma forma de declarar uma função sem ter que utilizar diversas linhas de código é usar a expressão lambda.
soma = lambda *nums: sum(nums)
dobro = lambda num: 2*num
print(soma(1, 2, 3))
print(dobro(3.14))##Obs: Em tópicos anteriores, criamos a função
somatoriomanualmente, mas ela já existe como uma das funções padrão do Python.
2.5 Trabalhando com arquivos
Nesta seção, veremos como trabalhar com arquivos. Veremos como abrir, escrever e ler arquivos com o Python.
###2.5.1 open
Para criar e ler arquivos, usamos a função open. Ela possui 2 argumentos:
file: caminho e nome do arquivo. Ex:C:\Users\satos\OneDrive\Área\ de\ Trabalho\arq_nome,./arq_nome. O ponto indica a pasta atual onde está sendo executado o programa.mode: existem alguns modos como podemos abrir um arquivo. Eles são especificados pelas seguintes strings.- “r”: read, lê o arquivo
- “w”: write, escreve o arquivo
- “a”: append, adiciona ao final do arquivo
- “b”: para abrir arquivos binários como imagens, vídeos e executáveis. Deve ser adicionado ao final de um dos modos acima. Ex:
"rb","wb"e"ab".
Depois que abrimos um arquivo e executamos as operações desejadas com ele, devemos fechá-lo para que não haja problemas posteriores. Para isso, usamos o close.
arquivo = open('texto.txt', 'w')
arquivo.write('Isto é um arquivo')
arquivo.close()
arquivo = open('texto.txt', 'r')
conteudo_arq = arquivo.read()
print(conteudo_arq)
arquivo.close()2.5.2 Escrevendo arquivos
Vimos anteriormente que podemos abrir o arquivo em modo w (write) ou a (append). Agora, veremos o que podemos fazer com isso. Usamos a função write para sobrescrever o arquivo (w) ou para adicionar conteúdo ao final do arquivo(a). Se o arquivo não existir, ele é criado.
arquivo = open('texto2.txt', 'w')
arquivo.write('Escrevendo no arquivo. ')
arquivo.close()
arquivo = open('texto2.txt', 'a')
arquivo.write('Adicionando conteúdo ao final do arquivo')
arquivo.close()
arquivo = open('texto2.txt', 'r')
print(arquivo.read())
arquivo.close()2.5.3 Lendo arquivos
Existem duas funções principais para ler arquivo.
read: lê o arquivo e retorna um string com o conteúdo do arquivo.readlines: lê o arquivo e retorna uma lista com as strings de cada uma das linhas
arquivo = open('texto3.txt', 'w')
arquivo.write('Arquivo de leitura\nUsamos as funções read e readlines para ler arquivos')
arquivo.close()
arquivo = open('texto3.txt', 'r')
print(arquivo.read())
arquivo.close()
arquivo = open('texto3.txt', 'r')
print(arquivo.readlines())
arquivo.close()###Obs:
\né um caracter de escape. Ele significa uma quebra de linha.
2.5.4 Trabalhando com arquivos
Nos últimos tópicos, tivemos que chamar a função open e close diversas vezes. Para que não dependamos disso, usaremos a estrutura with .... as. Nela, uma variável temporária será criada para manipularmos o arquivo. Com isso, não precisamos usar a função close.
with open('arquivo4.txt', 'w') as arq:
arq.write('Arquivo dentro de with as')
with open('arquivo4.txt', 'r') as arq:
print(arq.read())2.6 Programação Orientada a Objetos
Na história da programação, existiram diversos paradigmas. Por exemplo, os que vimos até agora foram: * Estruturada: Utiliza apenas das estruturas de controle para criar o código * Funcional: Utiliza funções para modularizar o código
Nesta seção, abordaremos um novo e muito famoso paradigma, o paradigma da orientação a objetos. Ele é muito importante para o Python, onde tudo que criamos é um objeto, e para o Manim, que trabalha com esse paradigma.
###2.6.1 Conceitos iniciais
O paradigma da Programação Orientada a Objetos (POO) foi criado por Alan Kay e tinha como objetivo aproximar o mundo real do mundo da programação.
Mas o que são objetos? > Em POO, podemos definir objetos como qualquer coisa concreta ou abstrata que possui: * propriedades/atributos: coisas que o objeto tem * comportamento/métodos: coisas que o objeto faz * estado atual: como o objeto está
Por exemplo, imaginemos um carro. Ele possui as seguintes características. * atributos: cor, modelo, tamanho, motor, etc * métodos: ligar, desligar, acelerar, desacelerar, etc * estado atual: parado, a 0 km/h, a 20 km/h, etc
A Orientação a Objetos possui 4 pilares: * Abstração: apenas aspectos importantes do objeto são extraídos para uma classe * Encapsulamento: ter acesso direto aos dados é perigoso, por isso, restringimos seu acesso * Herança: objetos podem herdar atributos e métodos de outros objetos * Polimorfismo: métodos herdados de outros objetos podem ter diferentes comportamentos
Veremos o que essas definições significam.
###2.6.2 Objeto e classe
Podemos pensar num objetos como uma variável cujo tipo é a classe. Nela, podemos definir seus atributos, que são variáveis que ela possui, e seus métodos, que são funções que ela pode chamar.
# Criando classe
class Carro:
# Definindo atributos da classe
cor = "preto"
modelo = "Gol"
velocidade_atual = 0
# Definindo método acelerar da classe
def acelerar(self):
self.velocidade_atual += 10
# Definindo método desacelerar da classe
def desacelerar(self):
self.velocidade_atual -= 10Acima, criamos uma classe chamada Carro com * atributos: cor, modelo e velocidade, * métodos: acelerar e desacelerar.
Obs: todos os métodos da classe devem ter o parâmetro
self, que é um parâmetro que faz referência ao próprio objeto. No exemplo acima, só conseguimos mudar a velocidade do carro por causo do parâmetroself
Obs: Podemos definir atributos como variáveis de um objeto e método como funções de um objeto.
###Obs: as classes devem ser nomeadas com nomes começando com letra maiúscula. Ser for usada mais do que uma palavra no nome, a separação das palavras é feita iniciando a primeira letra da próxima palavra em maiúsculo. Ex: MeuCarro
2.6.3 Construtor
Até agora, criamos uma classe, mas não um objeto. Antes de “instanciar” um objeto, precisamos definir seu construtor. O construtor de uma classe define o que ela fará quando for instanciada. Normalmente usamos o construtor para inicializar os seus atributos. Em Python, usamos o método __init__ para definir o construtor. Com o construtor definido, podemos instanciar um objeto a partir de sua classe.
# Criando classe
class Carro:
# Definindo atributos da classe
cor = "preto"
modelo = "Gol"
velocidade_atual = 0
# Definindo construtor da classe
def __init__(self, cor='preto', modelo='Gol'):
# Atribuindo valor aos atributos da classe
self.cor = cor
self.modelo = modelo
self.velocidade_atual = 0
# Definindo método acelerar
def acelerar(self):
# aumenta o valor da velocidade em 10
self.velocidade_atual += 10
# Definindo método desacelerar
def desacelerar(self):
# Diminui o valor da velocidade em 10
self.velocidade_atual -= 10
carro = Carro('vermelho', 'KA') # Instânciando um objeto carro
print(carro.cor) # chamando atributo cor de carro
print(carro.modelo) # chamando atributo modelo de carro
print(carro.velocidade_atual) # chamando atributo velocidade_atual de carroAcima, criamos uma classe que inicializa sua cor e modelo com parâmetros passados pelo construtor e inicializamos a sua velocidade atual em 0. Depois, imprimimos sua cor, modelo e velocidade.
Vamos demonstrar como o Manim usa classes e objetos. Criaremos uma cena animando um quadrado e transformando-o em um círculo.
%%manim -qm -v WARNING QuadradoPraCirculo
# Definindo classe da cena. Não se preocupe com o que está em parênteses
class QuadradoPraCirculo(Scene):
# Definindo método construct
def construct(self):
# Instanciando um objeto da classe Square, um quadrado
# Square() é o construtor da classe que nesse caso está sendo chamado e
# atribuído para a variável quadrado
quadrado = Square()
# Instanciando objeto da classe Circle
circulo = Circle()
# Animando quadrado com a classe Write
# Podemos passar oobjeto à uma função ou método sem atribuí-lo a uma variável
self.play(Write(quadrado))
# Transformando quadrado em círculo
self.play(ReplacementTransform(quadrado, circulo))2.6.4 Encapsulamento
Quando criamos um objeto, podemos acessar seus atributos diretamente. Porém, esse acesso não é uma boa ideia e pode até ser perigoso. É necessário esconder esses dados e criar métodos para acessar esses atributos.
Para esconder os dados colocamos um _ ou __ antes das variáveis.
class Pessoa:
def __init__(self, nome):
self.__nome = nome
pessoa = Pessoa('Vitor')
print(pessoa.__nome)Como podemos observar, ao colocarmos __, não é mais possível acessar o atributo de fora da classe. Para acessá-la, usaremos o property. Chamamos esse método de método acessor ou mais conhecido como getter.
class Pessoa:
def __init__(self, nome):
self.__nome = nome
@property
def nome(self):
return self.__nome
pessoa = Pessoa('Vitor')
print(pessoa.nome)Agora, podemos acessar o atributo nome de pessoa, mas não podemos modificá-lo. Para isso, usaremos o <nome da propriedade>.setter. Esse método se chama método modificador ou mais conhecido como setter.
class Pessoa:
def __init__(self, nome):
self.__nome = nome
@property
def nome(self):
return self.__nome
@nome.setter
def nome(self, nome):
self.__nome = nome
pessoa = Pessoa('Vitor')
pessoa.nome = 'Eric'
print(pessoa.nome)Com isso, podemos modificar o atributo __nome. Encapsulamos atributos para manter a segurança. O método getter retorna apenas uma cópia do valor do atributo e não o atributo em si.
2.6.5 Herança
Com a herança, podemos compartilhar funcionalidades entre classes. Quando criamos uma classe, podemos herdar seus atributos e métodos de outra classe. Chamamos a classe que compartilha os atributos e métodos de classe pai. Chamamos a classe que herda os atributos e métodos de classe filha. Usamos esse conceito quando diversas classes possuem algo em comum.
Por exemplo, temos classes cachorro e gato. Todas elas possuem o atributo nome. Em vez de criar um atributo nome em todas essas classes, podemos criar uma classe animal com atributo nome e todas as outras classes irão herdar dessa classe. Neste caso, animal é a classe pai e as demais são as classe filhas.
Para que as classes filhas herdem da classe pai, deve-se colocar a classe pai entre parenteses na frente da classe filha.
class Animal:
def __init__(self, nome):
self.nome = nome
class Cachorro(Animal):
def latir(self):
print('Au au!')
class Gato(Animal):
def miar(self):
print('Miau!')
cachorro = Cachorro('Fido')
print(cachorro.nome)
cachorro.latir()
gato = Gato('Happy')
print(gato.nome)
gato.miar()Como podemos observar, ao criar um cachorro e um gato, podemos acessar o atributo nome de cada um deles pois ambos herdam de Animal.
Também podemos acessar a classe pai dentro da classe filha usando o método super. Usamos isso para chamar métodos da classe pai.
class Animal:
def __init__(self, nome):
self.nome = nome
def get_nome(self):
return self.nome
class Cachorro(Animal):
def latir(self):
print(f'{super().get_nome()}: Au au!')
class Gato(Animal):
def miar(self):
print(f'{super().get_nome()}: Miau!')
cachorro = Cachorro('Fido')
cachorro.latir()
gato = Gato('Happy')
gato.miar()2.6.6 Polimorfismo
Outro conceito importante na POO é o polimorfismo. Basicamente, podemos modificar o comportamento de uma função da classe pai. Assim, diversas classe filhas possuem a mesma assinatura (nome), mas fazem coisas diferentes, embora semelhantes. Ou seja, é possível sobrescrever métodos das classes pai.
Do exemplo anterior, podemos criar um método acelerar na classe pai e mudá-lo na classe filha.
class Veiculo:
def __init__(self):
self.velocidade_atual = 0
def acelerar(self):
self.velocidade_atual += 1
class Carro(Veiculo):
def acelerar(self):
self.velocidade_atual += 10
class Moto(Veiculo):
def acelerar(self):
self.velocidade_atual += 20
carro = Carro()
carro.acelerar()
print(carro.velocidade_atual)
moto = Moto()
moto.acelerar()
print(moto.velocidade_atual)Como podemos observar, a classe Veiculo possui o método acelerar, mas as classes filhas modificam o comportamento desse método.
2.6.7 Operadores mágicos
Em vez de chamarmos métodos, podemos usar operadores como +, -, *, /, entre outros. Para isso, usamos operadores mágicos. Por exemplo, se tivermos uma classe Vetor, não podemos apenas usar o sinal de + para somar 2 vetores. Podemos usar o método __add__ para isso.
class Vetor:
def __init__(self, x, y):
self.x = x
self.y = y
def __add__(self, other: 'Vetor'):
return Vetor(self.x + other.x, self.y + other.y)
def __str__(self):
return f'[x: {self.x}, y: {self.y}]'
v1 = Vetor(1, 2)
v2 = Vetor(3, 4)
v3 = v1 + v2
print(v3)Podemos utilizar os seguintes operadores mágicos: * __sub__ para - * __mul__ para __truediv__ para / * __floordiv__ para // * __mod__ para % * __pow__ para ** * __and__ para & * __xor__ para ^ * __or__ para | * __lt__ para < * __le__ para <= * __eq__ para == * __ne__ para != * __gt__ para > * __ge__ para >= * __len__ para len() * __getitem__ para indexação * __setitem__ para atribuir valor a elementos indexados * __delitem__ para deletar valores indexados * __iter__ para iteração de objetos * __contains__ para in * __str__ para representação do objeto em string * __repr__ para representação do objto em string oficial * __init__ para instanciação da classe em objeto
###Obs: podemos utilizar o método
__dir__para visualizar todos os métodos de uma classe.
2.6.8 Métodos estáticos e de classe
Às vezes queremos executar um método de um objeto sem ter que instanciar a classe em objeto. Para isso, usamos métodos estáticos e de classe. Usamos decoradores para chamá-los.
class Retangulo:
def __init__(self, largura, altura):
self.largura = largura
self.altura = altura
def __str__(self):
return f'largura: {self.largura} altura: {self.altura}'
@classmethod
def novo_quadrado(cls, tamanho_lado):
return cls(tamanho_lado, tamanho_lado)
@staticmethod
def iniciar_quadrado():
print('Iniciando quadrado')
Retangulo.iniciar_quadrado()
print(Retangulo.novo_quadrado(2))###Obs: a diferença entre o método de classe e o método estático é que o de classe tem como primeiro parâmetro
clsque é o construtor da classe enquanto o método estático não tem.
Funções como objetos
Funções também são objetos. Elas podem ser atribuídas a variáveis passando apenas seu nome sem parenteses. Isso pode ser útil para passarmos funções como argumentos de outras funções.
# Definindo função que tem uma função como argumento
def printar_resultado(func, *args):
# Printando o retorno da função onde passamos parâmetros necessários
print(func(*args))
# Definindo função que será passada para outra função
def soma(num1, num2):
return num1 + num2
# Atribuindo a função printar_resultado a variável printar
printar = printar_resultado
# Chamando a função printar_resultado que armazenamos em printar
printar(soma, 1, 2)32.6.10 POO no Manim
Agora, vamos demonstrar como a POO é aplicada no Manim. Vamos criar uma animação que ilustra a manipulação de uma equação de 1\(^o\) grau para determinar o valor da incógnita.
%%manim -qm -v WARNING Formula
# Criando uma classe para a cena da animação
# Herda da classe Scene
class Formula(Scene):
# Sobrescrevendo método construct de Scene
def construct(self):
# Instanciando objetos MathTex, ou seja, chamando o construtor de MathTex
# MathTex são objetos gráficos para expressões matemáticas
eq1 = MathTex('2x + 3 = 0').scale(3)
eq2 = MathTex('2x = -3').scale(3)
eq3 = MathTex('x = -\\frac{3}{2}').scale(3)
# Chamando método play da superclasse Scene
# play é o método que anima os objetos gráficos
self.play(Write(eq1)) # escrevendo equação
self.play(TransformMatchingShapes(eq1, eq2)) # manipulando equação passo 1
self.play(TransformMatchingShapes(eq2, eq3)) # manipulando equação passo 2Nesse exemplo, vimos um exemplo dos tópicos: * Objeto e classe * Construtor * Herança * Polimorfismo
Não usamos os outros, mas eles podem aparecer em outros códigos.
##2.7 Bibliotecas
Utilizamos bibliotecas para modularizar o código e usar funcionalidades de terceiros. No nosso caso, usaremos a biblioteca Manim para as animações mas, antes, entenderemos como elas são criadas e como instalá-las.
###2.7.1 O que são bibliotecas?
Bibliotecas são arquivos com códigos que serão utilizados por outros códigos. É um conjunto de classes e funções para ajudar a desenvolver programas de forma mais fácil, simples e rápida.
###2.7.2 Como importar bibliotecas
Para importar uma biblioteca, utilizamos a palavra-chave import. Ao importarmos, a biblioteca é tratada como um objeto e podemos chamar suas funções ou objetos. Vamos importar a biblioteca numpy.
import numpy
vetor = numpy.array([1, 2])
print(vetor)Podemos renomear a biblioteca utilizada no nosso código. Vamos renomear numpy para np.
import numpy as np
vetor = np.array([1, 2])
print(vetor)Se quisermos algo que está dentro da biblioteca, usamos a palavra-chave from. Importaremos pyplot de matplotlib e o renomearemos para plt.
from matplotlib import pyplot as plt
f = lambda x: 2*x
x = [1, 2, 3]
y = [f(i) for i in x]
plt.plot(x, y)
plt.show()2.7.3 Como criar sua própria biblioteca
Para criar uma biblioteca, basta criar um arquivo Python com as funcionalidades desejadas. Para importá-lo, basta usar o import com o nome do arquivo.
Por exemplo, se criarmos o arquivo bib.py, ele será importado com:
import bibPara criar bibliotecas em uma pasta, é necessário criar um arquivo chamado __init__.py e para importá-lo, basta usar o import no nome da pasta.
Por exemplo, se criarmos uma pasta bib, precisamos criar um arquivo __init__.py e importá-lo com:
import bib2.7.4 args e kwargs
Nas bibliotecas, exitem muitas classes e hierarquias de classe, várias classes pais e suas filhas. Com isso, para criar os construtores, precisa-se de muitos argumentos. Para que não haja argumentos em excesso, usamos o args e kwargs. Já utilizamos o args em tópicos passados. O kwargs permite que utilizemos parâmetros nomeados passando dicionários. Esses dois parâmetros são muito usados no Manim.
class Veiculo:
def __init__(self, velocidade, cor, comprimento, altura, largura):
self.velocidade = velocidade
self.cor = cor
self.comprimento = comprimento
self.altura = altura
self.largura = largura
class Carro(Veiculo):
def __init__(self, marca, modelo, *args, **kwargs):
super().__init__(*args, **kwargs)
self.marca = marca
self.modelo = modelo
def __str__(self):
return f'marca: {self.marca} modelo: {self.modelo}'
carro = Carro(marca='Ford', modelo='KA', velocidade=0, cor='vermelho', comprimento=4, altura=1.5, largura=2)
print(carro)Com isso, não precisamos digitar o nome de todos os argumentos no construtor. Muitas bibliotecas externas também fazem como o Manim.
###2.7.5 pip
Para instalar bibliotecas de terceiros, utilizamos o gerenciador de pacotess pip. Com ele, podemos instalar, desinstalar e gerenciar bibliotecas listadas no PyPI (Python Package Index). As bibliotecas listadas no PyPI são chamados pacotes e são todos open source, ou seja, livre para uso não comercial dependendo de sua licença.
Para instalar pacotes, utilizamos o comando:
pip install <nome do pacote>Para desinstalar pacotes, utilizamos o comando:
pip uninstall <nome do pacote>Para listar pacotes instalados, utilizamos o comando:
pip listPara criar um arquivo para exportação com todos os pacotes usados, utilizamos o comando:
pip freeze > requirements.txtPara importar pacotes do requirements.txt, utilizar o comando:
pip install -U -r requirements.txt2.7.6 venv
Conforme vamos instalando bibliotecas, todos os scripts usados para fazer as animações podem ver todas as bibliotecas. Isso pode deixar o projeto da animação desorganizado. Para isso, utilizamos ambientes virtuais onde instalamos as bibliotecas apenas nesse ambiente. Para criarmos esses ambientes, usaremos a virtualenv ou venv.
A venv já vem por padrão desde o Python 3.3. Para criar um ambiente virtual, usar o comando no terminal
python -m venv <nome do ambiente>Para ativar o ambiente depois de criado, usar o comando
<nome do ambiente>/Scripts/activateCom isso, sempre que instalarmos novos pacotes, eles serão instalados dentro desse ambiente virtual. Note que ele irá criar uma estrutura de pastas com: * Include * Lib: onde as bibliotecas serão instaladas * Scripts: onde o script de inicialiação da venv será criada e onde uma versão do Python será instalada
Para mais informações, consultar a documentação da venv.
###2.7.7 requirements
No tópico pip, vimos como exportar pacotes usados, mas não explicamos o que isso significa. No Python, podemos salvar todas as bibliotecas usadas em um arquivo requirements.txt e se alguém precisar instalar todos esses pacotes, basta usar o comando.
pip install -U -r requirements.txt###Obs:
requirements.txté o nome padrão desse arquivo
2.7.8 numpy
Uma biblioteca muito utilizada no Manim é o numpy. Ela permite a criação de listas mais rápidas, vetores que são utilizados na biblioteca. Para criar um vetor, basta usar o comando array.
import numpy as np
vetor = np.array([1, 2, 3])
print(vetor)Também existem outras funções e objetos nessa biblioteca. Alguns exemplos são dados a seguir: * arange: podemos enxergá-lo como um range que aceita números reais em vez de apenas inteiros * linspace: especificamos o ponto de início e de fim e quantos números queremos entre eles
vetor1 = np.arange(0, 10, 0.1)
vetor2 = np.linspace(0, 1, 100)
print('Vetor1: ', vetor1)
print('Quantidade de números em vetor2: ', len(vetor2))
print('Vetor2: ', vetor2)Para instalar o numpy localmente, utilizamos o comando:
pip install numpyPara mais informações, consulte a documentação oficial do numpy
#
- Introdução ao Manim
Agora que vimos como trabalhar com o Python, desde coisas mais básicas(if, else, for) até mais avançadas (desempacotamento de tuplas, decoradores), vamos adiante com a biblioteca Manim.
3.1 Instalação Local
No momento, estamos usando o Manim no ambiente em nuvem do Google Colab, mas a maior parte dos projetos são criados localmente com arquivos Python. Para usar o Manim localmente, precisamos instalá-lo localmente. Vamos utilizar o ManimCE (Manim Community Edition).
Obs: não é necessário instalar o
Manimpara seguir com o Manual.
O Manim utiliza 2 softwares de linha de comando externos: * ffmpeg: o Manim usa esse software para manipular os vídeos criados. * Latex: usado para criar fórmulas e expressões matemáticas.
Para instalar no Windows, usaremos o gerencador de pacotes chocolatey. Para instalá-lo, abrir o powershell como administrador e usar o comando:
Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol = [System.Net.ServicePointManager]::SecurityProtocol -bor 3072; iex ((New-Object System.Net.WebClient).DownloadString('https://community.chocolatey.org/install.ps1'))Com o chocolatey instalado, podemos instalar o Manim simplesmente com o comando:
choco install manimceSe isso não funcionar, instalar o ffmpeg, Latex e Manim manualmente. * ffmpeg
choco install ffmpeg- Latex (manim-latex)
choco install manim-latexCom eles instalados, criar ambiente virtual (venv) e instalar o Manim com o comando:
pip install manimCaso ocorrer erro, recomeçar os passos.
Para mais informações consultar documentação.
Para instalar no Linux, em Ubuntu, Mint ou Debian, usar os comandos: * Dependências do Manim:
sudo apt update
sudo apt install libcairo2-dev libpango1.0-dev ffmpeg- Instalação do Python 3
sudo apt install python3-pip- Instalação do
Manim
pip3 install manimSe isso não funcionar, repetir os passos.
Para mais informações consultar documentação.
Para instalar no MacOS, usar os comandos: * Dependências do Manim
brew install py3cairo ffmpeg- Dependências adicionais
brew install cmake pango scipyManimpropriamente dito
pip3 install manimPara mais informações, consultar documentação.
##3.2 Estrutura da cena
Agora, começaremos a entender como o Manim funciona. Usamos código que o Manim interpreta e transforma em um vídeo. Para que ele identifique o que interpretar, usamos a classe Scene. Criamos uma classe que herda de Scene e o Manim o identifica. Para construir as animações, usamos o método construct herdado de Scene. Para o Manim identificar as animações a serem renderzadas, usamos o método play da superclasse Scene. Assim, o Manim encontra todas as classes que herdam de Scene, econtra o método construct e renderiza todos os métodos play. Já vimos alguns exemplos e vamos à mais um.
%%manim -qm -v WARNING Cena
# Definindo Cena
class Cena(Scene):
# Definindo método construct
def construct(self):
# Definindo objetos da cena
texto = Text('Bem-Vindo ao').scale(2)
manim_logo = VGroup(
MathTex(r'\mathbb{M}').scale(7).set_color('#ece6e2').shift(2.25 * LEFT + 1.5 * UP),
Circle(color='#81b29a', fill_opacity=1).shift(LEFT),
Square(color='#454866', fill_opacity=1).shift(UP),
Triangle(color='#e07a5f', fill_opacity=1).shift(RIGHT)
).move_to(ORIGIN)
# Chamando animações usando o método play
self.play(Write(texto))
self.play(FadeOut(texto))
self.play(FadeIn(manim_logo))
self.play(FadeOut(manim_logo))
3.3 Parâmetros de linha de comando
Aqui no Google Colab, utilizamos células mágicas, que são aquelas que começam com %% para renderizar a cena. Para renderizar localmente, usamos a linha de comando, também conhecido como cmd no Windows e terminal no Linux e MacOS. Para renderizar um vídeo, usamos o comando:
manim <nome do arquivo> <nome da animação> <opções><nome do arquivo>: nome do arquivo. Tem que ser um script Python, ou seja, um arquivo com terminação.py.<nome da animação>: nome da classe que herda deScene. Se não for especificado, é pedido para o usuário escolher a cena a ser renderizada.Opções: parâmetros utilizados para alterar configurações de renderização:-p: (preview). Abre o vídeo em um programa instalado no computador.-q: (quality) especifica qualidade da animação.-l: (low). Qualidade baixa.-m: (medium). Qualidade média.-h: (high). Qualidade alta.-k: (4k). Qualidade de 4k.
-s: renderiza o último frame (quadro) em uma imagem.-i: renderiza um gif.
Por exemplo, para renderizar a animação em qualidade baixa, usamos o comando:
manim <nome do arquivo> -pqlPara renderizar a imagem do estado final da animação, usar o comando:
manim <nome do arquivo> -sPara informações adicionais, consultar documentação
#
- Mobjects
No Manim, existem 3 blocos de construção principais: * Mobject: objetos gráficos a serem renderizados * Animation: animações propriamente ditas * Scene: cena onde as animações ficam
Elas são todas classes que constituem a animação. Nesta parte, veremos alguns Mobjects frequentemente usados.
Para visualizar todos os Mobjects, consultar documentação.
##
4.1 Text
O primeiro Mobject que veremos é o Text. Para criar um, usamos seu construtor onde passamos o texto e alguns outros parâmetros.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
texto = Text('Isso é um texto')
self.add(texto)
Obs: usamos o método
addpara adicionar um objeto gráfico à cena resultando em apenas uma imagem.
Podemos mudar a fonte do texto usando o argumento font.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
texto = Text('Isso é um texto', font='Noto Sans')
self.add(texto)
Para mudar a formatação do texto em normal e itálico, usar o argumento slant com os parâmetros NORMAL e ITALIC.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
texto = Text('Texto itálico', slant=ITALIC)
self.add(texto)
Também é possível mudar a cor com o argumento color.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
texto = Text('Texto vermelho', color=RED)
self.add(texto)
Também podemos mudar a cor do texto com o MarkupText. Ela renderiza um texto em formato Markup que é uma linguagem que permite formatar o texto. Para definir um bloco do texto que queremos editar, usamos as tags <span> com a propriedade fgcolor como no exemplo a seguir.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
text = MarkupText(f'all in red <span fgcolor="{YELLOW}">except this</span>', color=RED)
self.add(text)
Tamém podemos criar gradientes de cores com o argumento gradient.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
text = MarkupText('Isso é um texto', gradient={RED, GREEN, BLUE})
self.add(text)
4.2 Latex
Agora que vimos como usar textos no Manim, vamos ver como utilizar as fórmulas e expressõers matemáticas. Para isso, usaremos o Latex, uma linguagem de marcação muito usada para escrever artigos científicos e que permite escrever documentos e renderizar expressões matemáticas. Para aprender mais sobre o Latex, consulte o seguinte material.
Se você não tem muita prática com o Latex, você pode usar o seguinte site para criar as fórmulas matemáticas.
Para renderizar as equações aqui no Google Colab, colocamos a expressão entre $$. Vamos ver algumas expressões que podem ser criadas no Latex.
- mutiplicação - \(\cdot\)
- três pontos
- divisão - \(\div\)
- somatório - \(\sum\)
- limite - _{x a} f(x) \(\lim_{x \rightarrow a} f(x)\)
- seta direita - \(\rightarrow\)
- seta esquerda - \(\leftarrow\)
- menor ou igual - \(\leq\)
- maior ou igual - \(\geq\)
- aproximado - \(\approx\)
- pertence - \(\in\)
- não pertence - \(\notin\)
- raíz quadrada - \(\sqrt{x}\)
- raíz - \(\sqrt[n]{x}\)
- fração - \(\frac{a}{b}\)
- intersecção - \(\cap\)
- união - \(\cup\)
- vezes - \(\times\)
- pi - \(\pi\)
- theta - \(\theta\)
- Quebra de linha - \\
- Equações -
x &= 3 + 2 + 1
x &= 5 + 1
x &= 6
\(f(x) = 3 + 2 + 1\\ = 5 + 1 \\ = 6\)
- Matrizes -
4.3 MathTex
Agora que sabemos usar o Latex para expressões matemáticas, vamos entender como usá-las no Manim. Para criar um objeto gráfico, usamos o objeto MathTex que será renderizado na tela, passando o códiog Latex.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
text = MathTex(r'f(x) &= 3 + 2 + 1\\ &= 5 + 1 \\ &= 6')
self.add(text)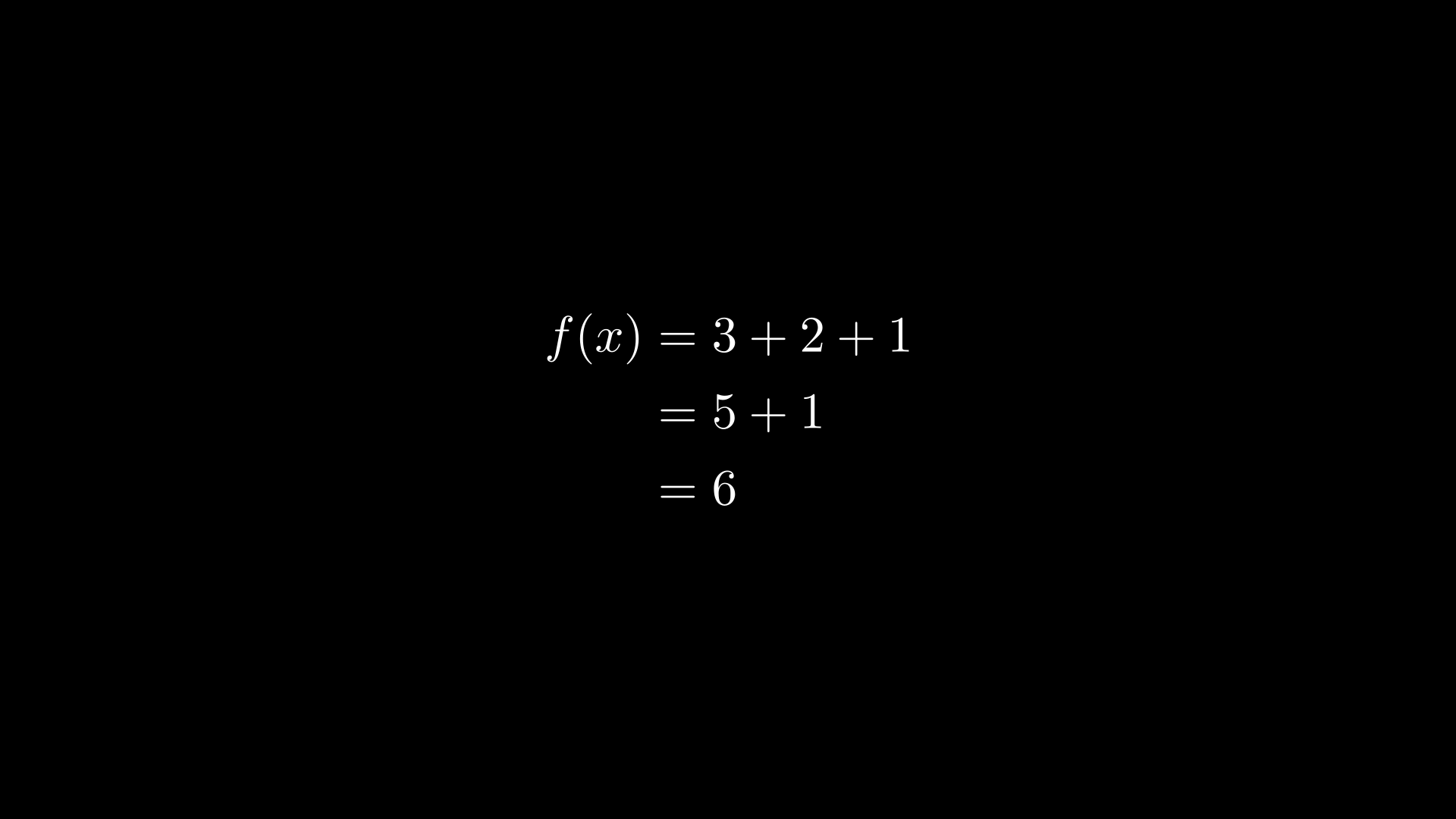
Também podemos separar um MathTex como uma lista separando os textos por vírgulas.
%%manim -qm -v WARNING Texto
class Texto(Scene):
def construct(self):
texto = MathTex(r'\lim_{a \rightarrow 0} \frac{f(x+a) - f(x)}{a} = ', r'\frac{df(x)}{dx}').scale(1.5)
# Animando a parte do limite
self.play(Write(texto[0]))
# Pausa de 1 segundo
self.wait()
# Animando a parte da derivada
self.play(Write(texto[1]))
4.4 Tex
O Latex também possui o modo texto. Usamos o comando \text{} para isso. No Manim, podemos usar o Tex para isso. Podemos utilizá-lo com listas igual ao MathTex.
%%manim -s -v WARNING Texto
class Texto(Scene):
def construct(self):
text = Tex('Isso é um Tex', gradient={RED, GREEN, BLUE})
self.add(text)
4.5 geometry
Agora, veremos alguns objetos geométricos como retângulos e retas.
###Obs: não abordaremos todos os objetos geométricos. Para mais informações, consulte documentação.
4.5.1 Square
Para começar vamos ver o objeto Square, ou seja, quadrado. Passamos o tamanho do lado para ele.
%%manim -s -v WARNING Quadrado
class Quadrado(Scene):
def construct(self):
quadrado = Square(side_length=3)
self.add(quadrado)
4.5.2 Rectangle
O Rectangle é usado para criar um retângulo. Passamos os tamanhos de seus lados.
%%manim -s -v WARNING Retangulo
class Retangulo(Scene):
def construct(self):
retangulo = Rectangle(height=2, width=3)
self.add(retangulo)
4.5.3 Circle
Usamos o Circle para criar um círculo. Passamos o seu raio.
%%manim -s -v WARNING Circulo
class Circulo(Scene):
def construct(self):
circulo = Circle(radius=3)
self.add(circulo)
4.5.4 Ellipse
Usamos o Ellipse para criar uma elipse. Passamos os valores do semi-eixo maior e menor.
%%manim -s -v WARNING Elipse
class Elipse(Scene):
def construct(self):
elipse = Ellipse(height=3, width=4)
self.add(elipse)
4.5.6 Coordenadas no Manim
Antes de apresentarmos mais objetos, vamos entender como o sistema de coordenadas no Manim funciona.
No Manim, as coordenadas são dadas através de um numpy.array de 3 elementos que representam as coordenadas \(x\), \(y\) e \(z\). Mesmo em planos bidimensionais, são passadas as 3 coordenadas. Nesses casos, o terceiro elemento é passado como 0. Por exemplo: np.array([1, 2, 0])
Mesmo que o sistema de coordenadas esteja em numpy.array, ainda é possível utilizar listas ou tuplas de 3 elementos quando especificarmos a posição dos objetos gráficos na tela. As coordenadas funcionam no sistema \((x, y, z)\), ou seja, \((0, 0, 0)\) é o centro da tela. Se aumentarmos \(x\), movemos as coordenadas para direita e, se aumentarmos \(y\), movemos as coordenadas para cima.
Para facilitar e não ter que escrever as coordenadas, é possível usar direções (constantes) que especificam essas coordenadas de maneira mais “humana”. Existem as constantes: * RIGHT: np.array([1, 0, 0]) * LEFT: np.array([-1, 0, 0]) * UP: np.array([0, 1, 0]) * DOWN: np.array([0, -1, 0])
Podemos pensá-las como os vetores na matemática, ou seja, podemos somá-las e multiplicá-las por um número real.
Podemos observar as extremidades da tela no Manim com o seguinte código. Se não entender algo, não se preocupe pois vamos abordar o que não for abordado.
%%manim -s -v WARNING Reta
class Reta(Scene):
def construct(self):
def get_coords(mob: Mobject, direction: list):
text_coords = Text(f'({round(mob.get_x(), 2)}, {round(mob.get_y(), 2)})')
return text_coords.move_to(mob.get_center() + direction).scale(0.5)
up = Dot().to_corner(UP)
right = Dot().to_corner(RIGHT)
left = Dot().to_corner(LEFT)
down = Dot().to_corner(DOWN)
up_label = get_coords(up, 0.5*DOWN)
right_label = get_coords(right, 1.3*LEFT)
left_label = get_coords(left, 1.3*RIGHT)
down_label = get_coords(down, 0.5*UP)
self.add(up)
self.add(up_label)
self.add(right)
self.add(right_label)
self.add(left)
self.add(left_label)
self.add(down)
self.add(down_label)
4.5.7 Line
Usamos o Line para criar uma seta, informando as coordenadas de início e de fim.
%%manim -s -v WARNING Reta
class Reta(Scene):
def construct(self):
reta = Line(start=(-1, -2, 0), end=(1, 2, 0))
self.add(reta)
4.5.8 Arrow
Usamos o Arrow para criar uma seta, informando as coordenadas de início e de fim.
%%manim -s -v WARNING Seta
class Seta(Scene):
def construct(self):
seta = Arrow(start=2*DOWN+LEFT, end=UP+2*RIGHT)
self.add(seta)
4.5.9 Dot
Usamos o Dot para criar um ponto, especificando suas coordenadas.
%%manim -s -v WARNING Ponto
class Ponto(Scene):
def construct(self):
ponto = Dot(point=UP*RIGHT)
self.add(ponto)
4.6 Manipular Mobjects
Agora que vimos como criar Mobjects, veremos como manipulá-los, ou seja, mudar cor, posição, tamanho, girar, entre outros.
###
4.6.1 move_to
Uma das formas de mover um objeto é com o método move_to. Especificamos suas coordenadas e ele move o Mobject.
%%manim -s -v WARNING Mover
class Mover(Scene):
def construct(self):
ponto1 = Dot()
ponto1.move_to(2*UP)
ponto2 = Dot().move_to(2*DOWN)
self.add(ponto1)
self.add(ponto2)
4.6.2 next_to
Outra forma de mover objetos é com o next_to. Como o próprio nome já diz, “próximo à”. Ou seja, especificamos um objeto, em que sentido queremos deixar o objeto e a distância entre os objetos.
%%manim -s -v WARNING Mover
class Mover(Scene):
def construct(self):
quadrado = Square()
ponto = Dot().next_to(mobject_or_point=quadrado, direction=RIGHT, buff=0)
self.add(quadrado)
self.add(ponto)
4.6.3 shift
Outra forma de mover objetos é usando o shift. Ele move o objeto em relação à sua posição atual. É o método mais simples.
%%manim -s -v WARNING Mover
class Mover(Scene):
def construct(self):
quadrado = Square().shift(2*UP)
self.add(quadrado)
4.6.4 to_corner
A última forma de mover objetos que veremos é o to_corner. Ele move o objeto para um dos cantos da tela. Basta passar a posição e ele acha o canto.
%%manim -s -v WARNING Mover
class Mover(Scene):
def construct(self):
quadrado = Square().to_corner(LEFT+UP)
self.add(quadrado)
4.6.5 scale
Para mudar o tamanho dos objetos, usamos o método scale. Passamos um número que representa o quanto queremos aumentar o objeto. Se passarmos 2, o objeto aumentará 2 vezes.
%%manim -s -v WARNING Escala
class Escala(Scene):
def construct(self):
quadrado = Square().scale(2)
self.add(quadrado)
4.6.6 rotate
Também podemos girar um objeto com o rotate. Passamos o ângulo em radianos para o método e ele gira o objeto. Podemos usar o DEGREES para converter para graus.
%%manim -s -v WARNING Rotacionar
class Rotacionar(Scene):
def construct(self):
quadrado = Square().rotate(45*DEGREES)
self.add(quadrado)
4.6.7 set_color
Podemos alterar a cor dos objetos com o set_color. O Manim possui constantes com algumas cores pré-definidas. Também podemos especificar cores em hexadecimal.
Obs: Para mais informações, consultar documentação.
Obs: Para passar a cor em hexadecimal, usar uma ferramenta para escolher a cor.
%%manim -s -v WARNING Cor
class Cor(Scene):
def construct(self):
quadrado = Square().set_color(RED)
self.add(quadrado)
4.6.8 become
No Manim, quando alteramos os atributos de um objeto, nem sempre isso se reflete na tela. Para isso, usamos o método become que transforma um objeto em outro.
%%manim -s -v WARNING Tornar
class Tornar(Scene):
def construct(self):
quadrado = Square()
quadrado.become(Circle())
self.add(quadrado)
4.6.9 copy
Uma forma de criarmos cópias de objetos é com o método copy. Isso não é um método do Manim, mas do próprio Python. Todos os objetos possuem esse método.
%%manim -s -v WARNING Copia
class Copia(Scene):
def construct(self):
quadrado1 = Square().shift(DOWN)
quadrado2 = quadrado1.copy().shift(2*UP+2*LEFT)
self.add(quadrado1)
self.add(quadrado2)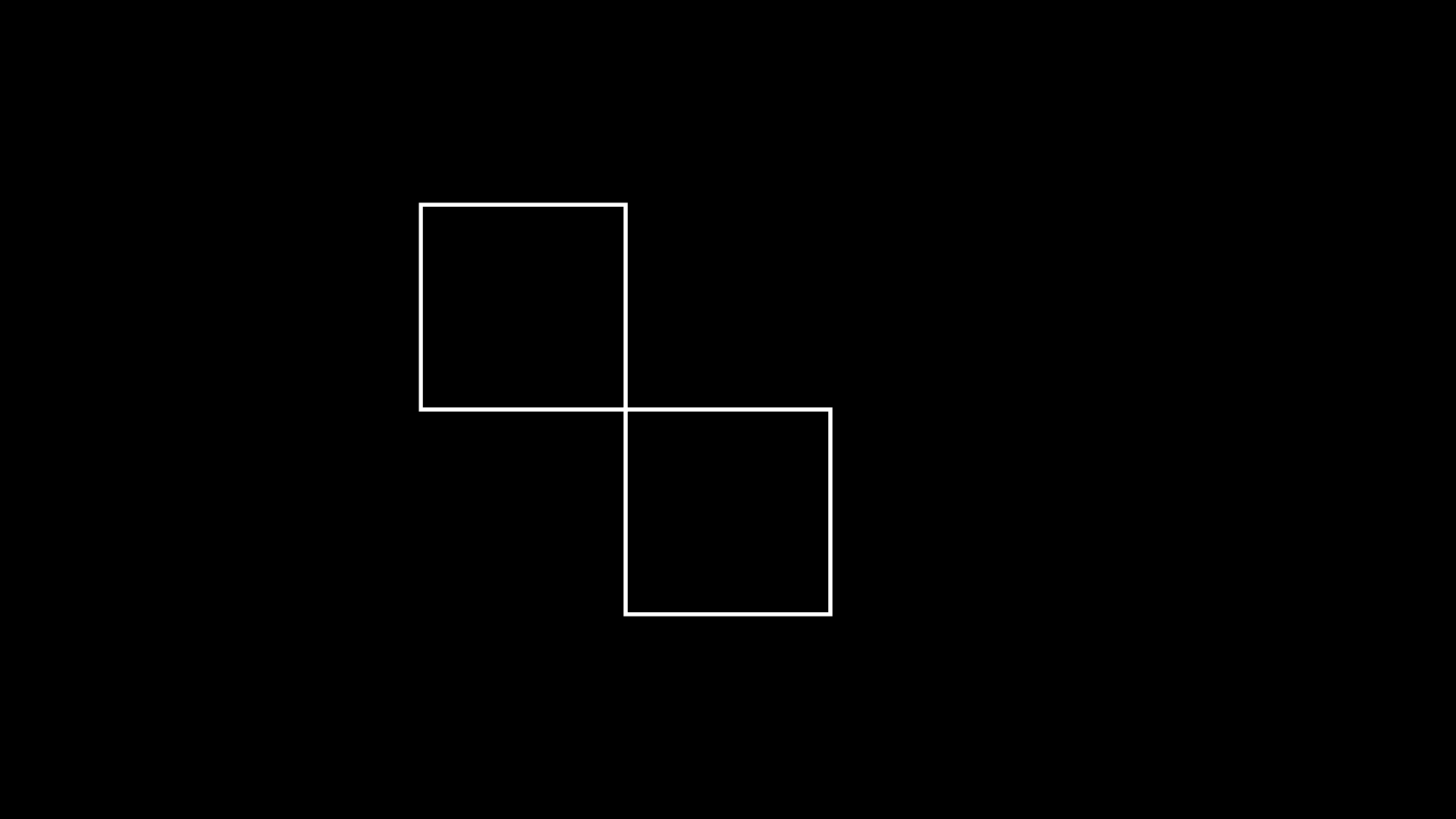
4.7 VGroup
É possível agrupar Mobjects usando listas. Entretanto, há um jeito melhor para fazer isso. Para criar um grupo de Mobjects, usamos o VGroup. Nele, colocamos todos os objetos que queremos agrupar. Ele é muito útil quando queremos manipular vários objetos que compõem um todo.
%%manim -s -v WARNING Grupo
class Grupo(Scene):
def construct(self):
# Definindo função da parábola
func = lambda x: x**2 - 2
# Criando um grupo de linhas que irá repesentar a parábola
parabola = VGroup(
# Usando o desempacotamento de listas
#para passar todas as linhas como parâmetro
*[
# Linha que começa em (i, f(i)) e termina em (i+0.1, f(1+0.1))
Line(
start=(i, func(i), 0),
end=(i+0.1, func(i+0.1), 0)
)
for i in np.arange(-2, 2, 0.1)
]
)
self.add(parabola)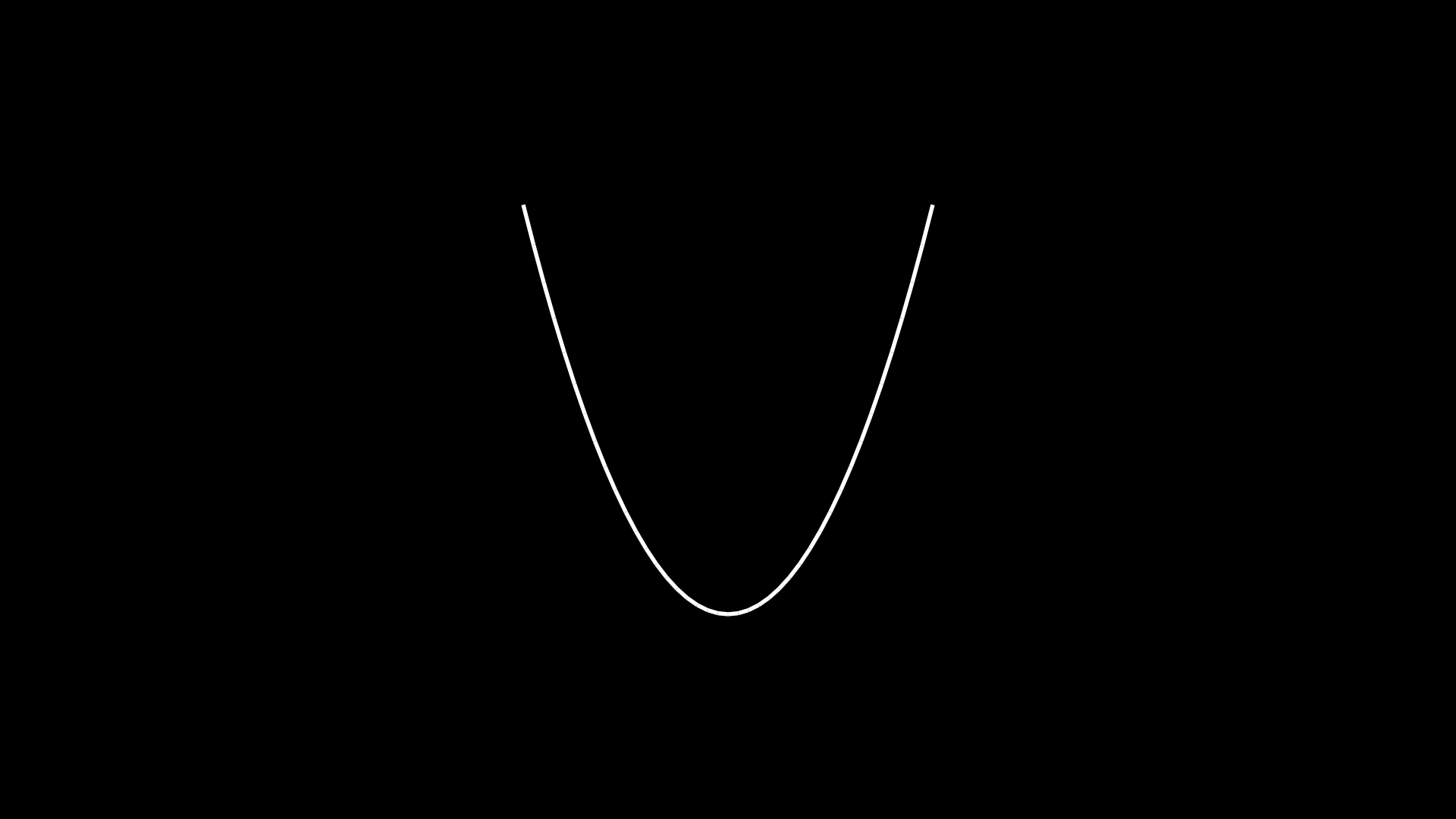
- Animações
Agora que vimos vários elementos gráficos, vamos começar com as animações. Como foi visto anteriormente, animamos uma cena utilizando o método construct. Dentro dele, chamamos o método play e a animação que queremos renderizar. Veremos essas animações nesta seção. Em todas elas, passamos o objeto que queremos animar e a animação faz o resto do trabalho. No play, também podemos passar um parâmetro run_time que é o tempo que a animação vai durar.
5.1 Write
A primeira animação que veremos é o Write. Ela anima um objeto com se estivesse escrevendo-o como o próprio nome diz.
%%manim -qm -v WARNING Escrever
class Escrever(Scene):
def construct(self):
texto = Text('Texto escrito').scale(2)
self.play(Write(texto), run_time=2)##Obs: É normal esquecer de passar a animação e passar apenas um Mobject pelo
play. Nesses casos, aparecerá um erro que alertará o usuário que não há animação sendo passada.
5.2 FadeIn
O FadeIn anima o objeto como se estivesse aparcendo na tela.
%%manim -qm -v WARNING Aparecer
class Aparecer(Scene):
def construct(self):
texto = Text('Texto apareceu').scale(2)
self.play(FadeIn(texto, run_time=2))
5.3 FadeOut
Ao contrário das animações que vimos até agora, o FadeOut faz o objeto gráfico desaparecer.
%%manim -qm -v WARNING Desaparecer
class Desaparecer(Scene):
def construct(self):
texto = Text('Texto desapareceu').scale(2)
self.play(FadeIn(texto), run_time=1)
self.wait()
self.play(FadeOut(texto), run_time=2)
5.3 Transform e ReplacementTransform
Agora, vamos ver animações que pegam objetos e os transformam em outros. O Transform e ReplacementTransform cumprem esse papel. Passamos o objeto inicial e o final.
%%manim -qm -v WARNING QuadradoParaCirculo
class QuadradoParaCirculo(Scene):
def construct(self):
quadrado = Square(side_length=2)
circulo = Circle(radius=2)
self.play(Write(quadrado))
self.play(Transform(quadrado, circulo))A diferença entre o Tranform e o ReplacementTransform é que, para manipular os objetos depois da transformação com o: * Transform: o objeto a ser manipulado no final da transformação deve ser o inicial * ReplacementTransform: o objeto a ser manipulado no final da transformação deve ser o final
%%manim -qm -v WARNING QuadradoParaCirculo
class QuadradoParaCirculo(Scene):
def construct(self):
quadrado1 = Square(side_length=2)
circulo1 = Circle(radius=2)
self.play(Write(quadrado1))
self.play(Transform(quadrado1, circulo1))
self.play(FadeOut(quadrado1))
quadrado2 = Square(side_length=2)
circulo2 = Circle(radius=2)
self.play(Write(quadrado2))
self.play(ReplacementTransform(quadrado2, circulo2))
self.play(FadeOut(circulo2))Se não fizermos isso, coisas estranhas acontecerão!
%%manim -qm -v WARNING QuadradoParaCirculo
class QuadradoParaCirculo(Scene):
def construct(self):
quadrado1 = Square(side_length=2)
circulo1 = Circle(radius=2)
self.play(Write(quadrado1))
self.play(Transform(quadrado1, circulo1))
self.play(FadeOut(circulo1))
quadrado2 = Square(side_length=2)
circulo2 = Circle(radius=2)
self.play(Write(quadrado2))
self.play(ReplacementTransform(quadrado2, circulo2))
self.play(FadeOut(quadrado2))5.4 Animações de manipulação
A manipulação de objetos, movendo-os ou alterando seus tamanhos, não acontece em forma de animação. Para animar esse tipo de manipulação, é necessário usar o atributo animate.
%%manim -qm -v WARNING QuadradoParaCirculo
class QuadradoParaCirculo(Scene):
def construct(self):
quadrado = Square(side_length=2)
self.play(Write(quadrado))
self.wait()
self.play(quadrado.animate.move_to(UP))Em outras versões do Manim como o Manimcairo e o ManimGL, passamos o método e seus parâmetros. Não conseguimos fazer isso aqui pois esse método foi depreciado. Mas podemos demonstrar como fazer isso com o objeto ApplyMethod.
%%manim -qm -v WARNING QuadradoParaCirculo
class QuadradoParaCirculo(Scene):
def construct(self):
quadrado = Square(side_length=2)
self.play(Write(quadrado))
self.wait()
self.play(ApplyMethod(quadrado.move_to, UP))5.5 Outras animações
Vimos diversas animações até agora, mas ainda existem diversas outras, basta explorá-las. Para mais informações consulte a documentação.
#
- Gráficos 2D
Alguns Mobjects que não vimos são os gráficos. Existem alguns objetos que os representam que veremos nesta parte.
#
6.1 NumberLine
O primeiro objeto que veremos é o NumberLine. Como o próprio nome já diz, ele representa uma linha (reta) de números (reais). Ela possui um construtor com diversos parâmetros, mas os principais são: * x_range: lista ou tupla com 3 parâmetros como se fosse o range onde o primeiro número é o número inicial, o segundo é o final e o terceiro é número de passos. * include_numbers: exibe os números na reta * length: tamanho da reta * include_tip: exibe uma seta ao final da reta
%%manim -s -v WARNING RetaReais
class RetaReais(Scene):
def construct(self):
reta_reais = NumberLine(
x_range=(-2, 6, 1),
include_numbers=True,
length=8
).scale(0.8)
self.add(reta_reais)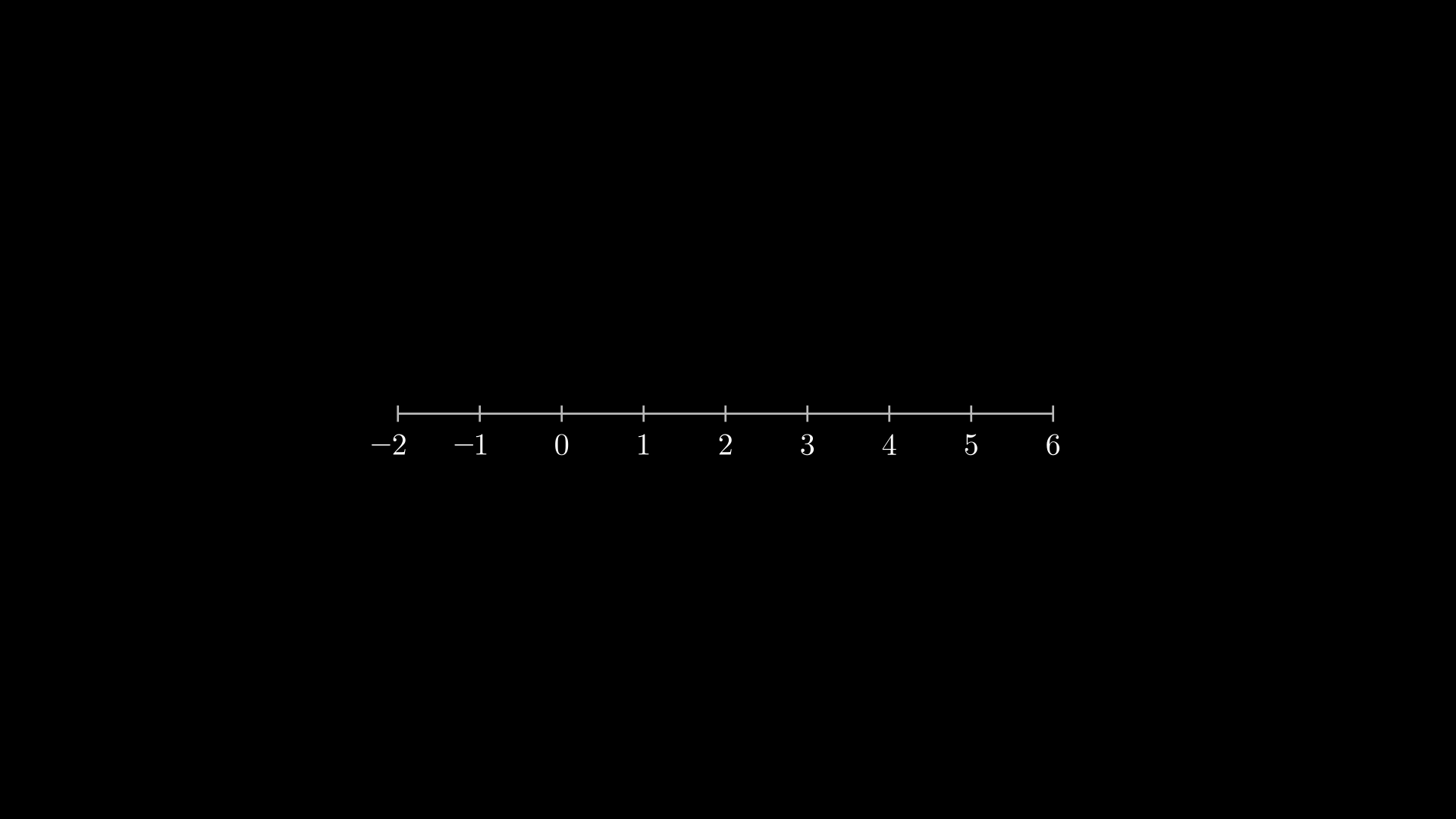
Temos alguns métodos úteis: * n2p: acrônimo para number to point. Transforma um número em uma lista de onde o ponto está na reta * get_number_mobject: retorna um Tex com o valor passado como parâmetro de acordo com a reta * add_labels: adiciona textos na reta. Útil para adicionar o nome do eixo como \(x\) ou \(y\)
%%manim -s -v WARNING RetaReais
class RetaReais(Scene):
def construct(self):
# Criando reta dos reais com uma seta à direita e adicionando label x e escalando em 0.8
reta_reais = NumberLine(include_tip=True).add_labels({7: 'x'}).scale(0.8)
# Criando ponto e movendo-o para a posição 1 da reta dos reais
ponto = Dot().move_to(reta_reais.n2p(1))
# Criando o número 2 na reta
numero = reta_reais.get_number_mobject(2)
self.add(reta_reais, ponto, numero)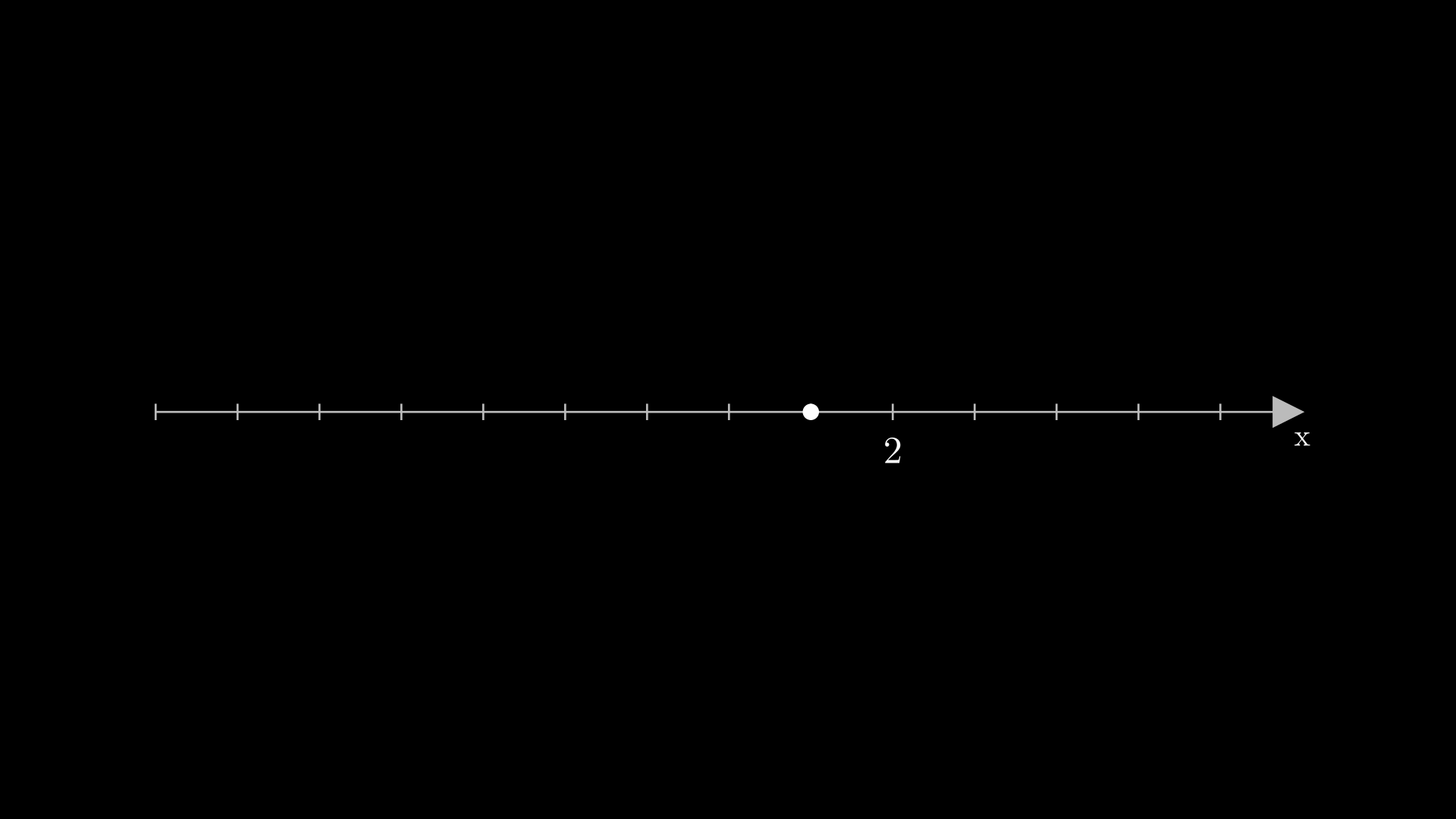
6.2 Axes
O NumberLine representa um eixo, já a classe Axes representa 2 eixos (perpendiculares), ou seja, o plano cartesiano. Possui argumentos parecidos com o do NumberLine, porém, existem os eixos \(x\) e \(y\). * x_range e y_range: funciona como o range, porém para os eixos \(x\) e \(y\) * x_length e y_length: funciona como o length, porém, para os 2 eixos * tips: funciona como o include_tip, porém, para ambos os 2 eixos * x_axis_config e y_axis_config: pode passar qualquer argumento de NumberLine em um dicionário e irá aplicar ao eixo \(x\) ou \(y\)
Não precisamos passar nenhum parâmetro pelo construtor pois todos os seus parâmetros são opcionais.
%%manim -s -v WARNING Eixos
class Eixos(Scene):
def construct(self):
eixos = Axes(
tips=True,
x_range=(-16, 16, 2),
y_range=(-8, 8, 2),
x_axis_config={'include_numbers': True},
y_axis_config={'include_numbers': True}
)
self.add(eixos)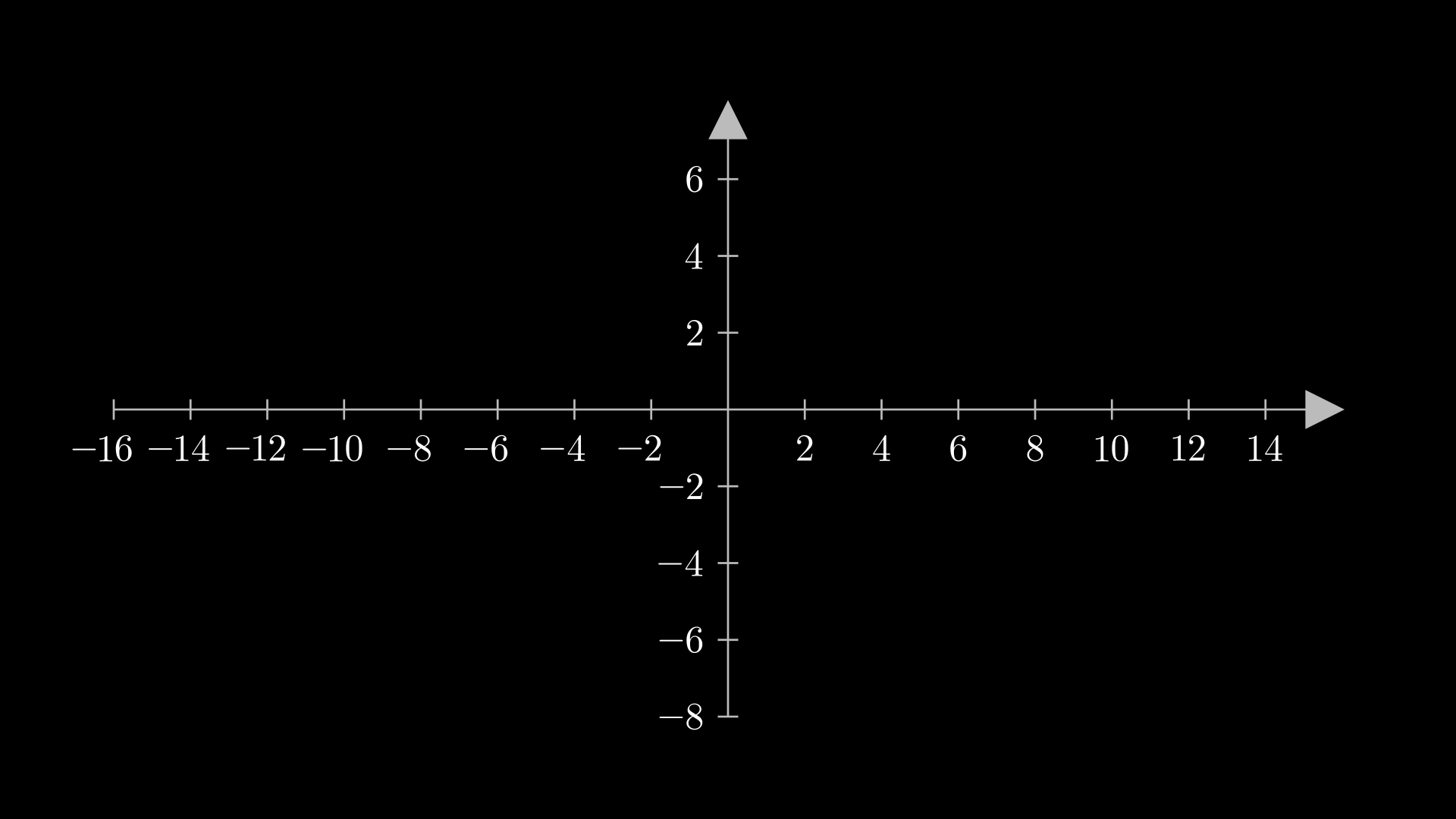
No código fonte, ele é criado utilizando 2 objetos NumberLine, ou seja, podemos pegar cada uma das retas que representam os eixos e usar seus métodos. Para isso, usamos o método get_axis. Ele retorna uma lista com os 2 NumberLine.
%%manim -s -v WARNING Eixos
class Eixos(Scene):
def construct(self):
eixos = Axes()
eixo_x = eixos.get_axes()[0].set_color(BLUE)
eixo_y = eixos.get_axes()[1].set_color(RED)
self.add(eixo_x, eixo_y)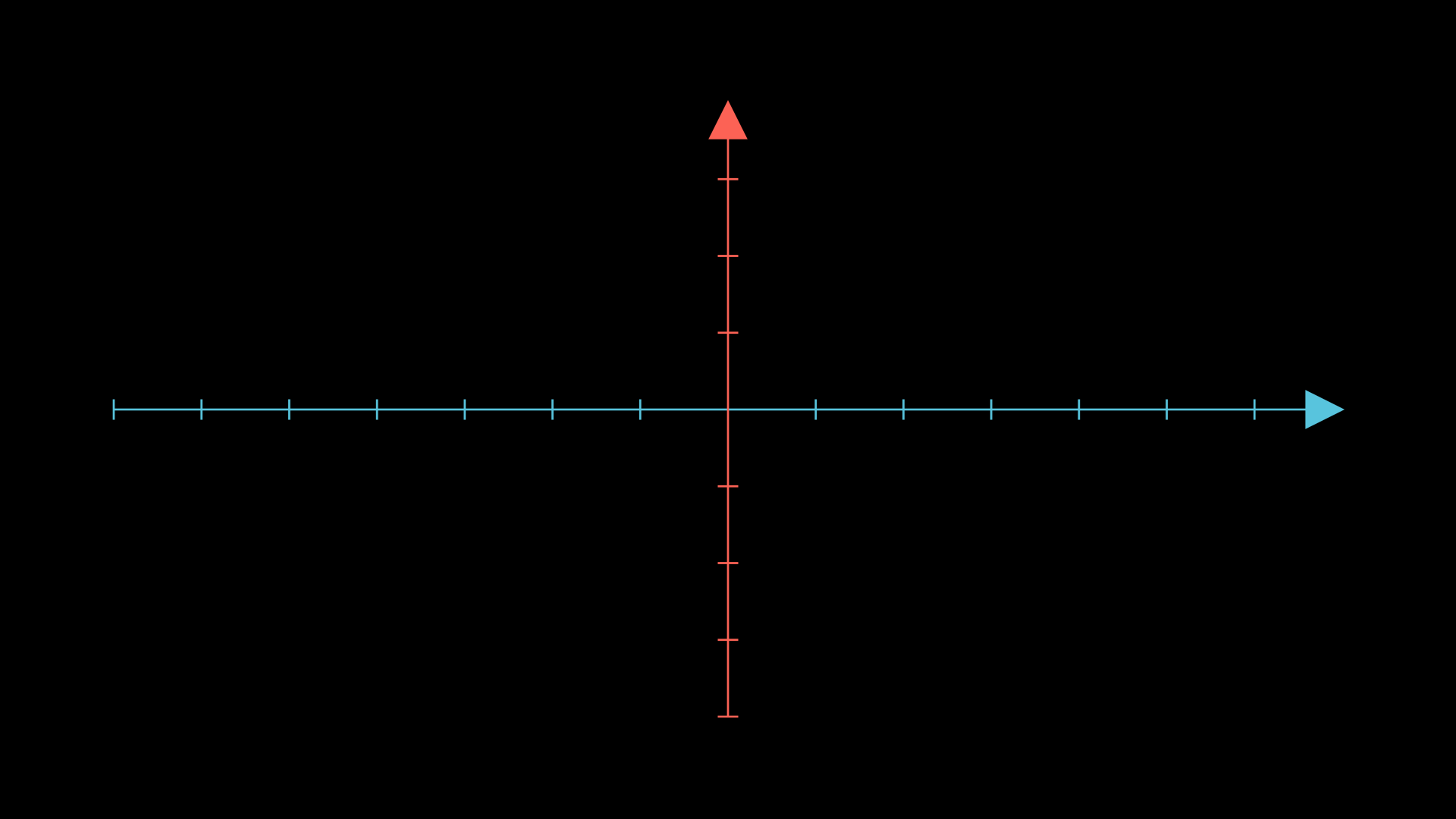
Ainda temos alguns métodos interessantes para utilizarmos. * c2p: passa coordenadas \(x\) e \(y\) e transforma em cordenadas do Manim * get_graph: passa uma função e retorna o gráfico da função * get_line_graph: passa 2 listas, uma com as coordenadas \(x\) e outra com as coordenadas \(y\) e retorna o gráfico com os pontos conectados por segmentos de retas * get_horizontal_line: passa as coordendas do ponto e retorna a linha horizontal até esse ponto * get_vertical_line: passa as coordenadas do ponto e retorna a linha vertical até esse ponto
%%manim -s -v WARNING Eixos
class Eixos(Scene):
def construct(self):
# Criando eixos
eixos = Axes(
x_axis_config={'include_numbers': True},
y_axis_config={'include_numbers': True}
)
# Criando ponto nas coordenadas (3, 3) de acordo com os eixos do gráfico
ponto = Dot().move_to(eixos.c2p(3, 3))
# Criando linha vertical entra os eixos e o ponto
v_line = eixos.get_vertical_line(ponto.get_center())
# Criando linha horizontal entre os eixos e o ponto
h_line = eixos.get_horizontal_line(ponto.get_center())
# Declarando função
f = lambda x: x**2 - 2
# Declarando pontos x
x = [i for i in range(-2, 3, 1)]
# declarando pontos y = f(x)
y = [f(i) for i in range(-2, 3, 1)]
# Criando gráfico de linha utilizando as listas x e y
line_graph = eixos.get_line_graph(x_values=x, y_values=y)
# Criando o gráfico de f automaticamente
graph = eixos.get_graph(f, x_range=(-2, 2))
self.add(eixos, ponto, v_line, h_line, line_graph, graph)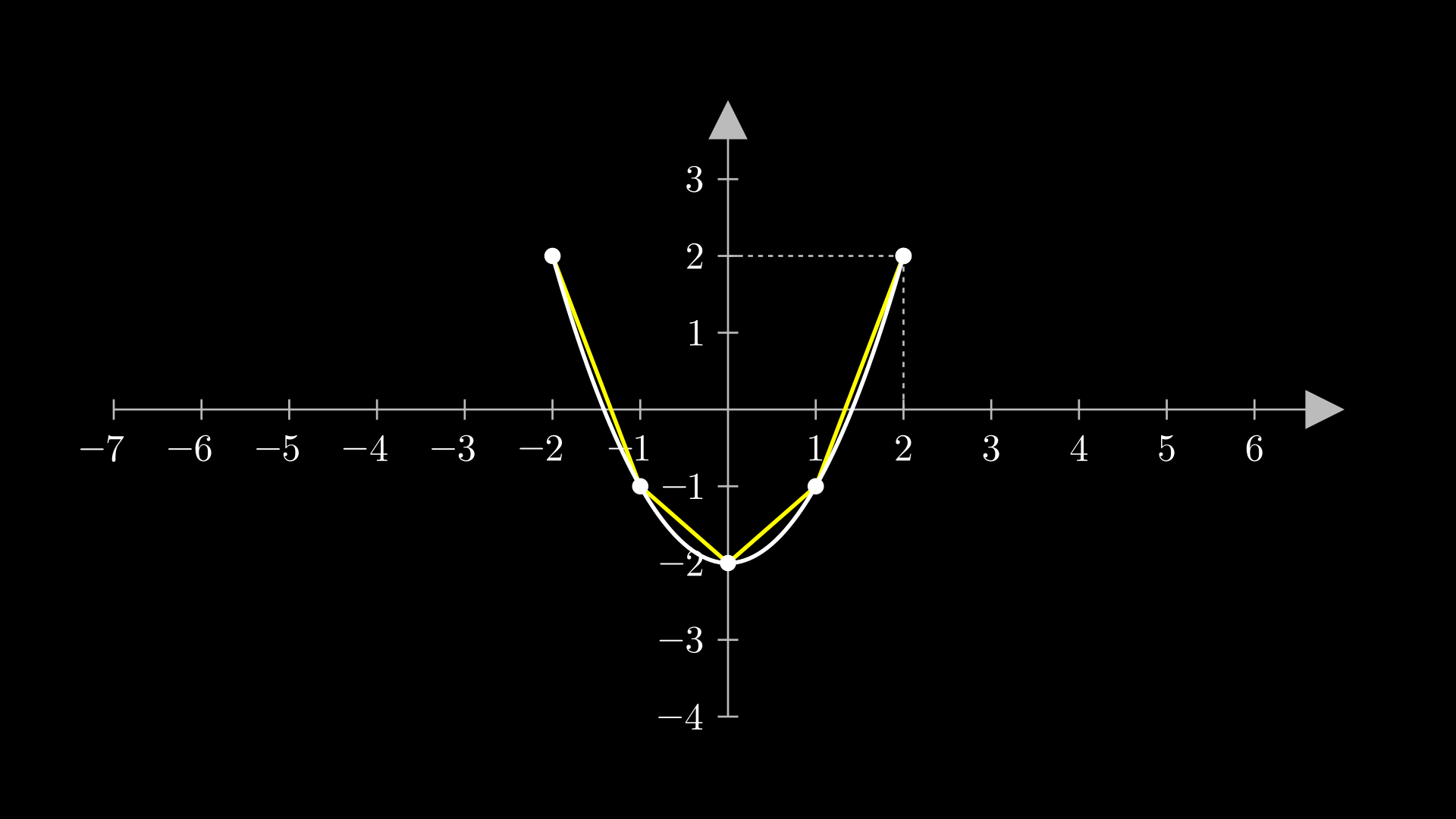
- Update functions
O Manim possui diversas animações pré-definidas, porém, é possível criar nossas próprias animações. Para isso, usamos as update functions.
##7.1 Animações frame a frame
As primeiras animações (como as de desenhos e filmes) eram feitas desenhando e gravando diversas imagens (ou mais popularmente conhecidas como frames), dando a sensação de movimento. Esse processo é feito até hoje! Entretanto, hoje em dia, existem ferramentas que automatizam uma parte deste processo. Esse tipo de processo também pode ser feito no Manim, utilizando o wait.
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
# Criando quadrado
quadrado = Square()
# adicionado quadrado à cena
self.add(quadrado)
# Adicionando 30 quadros à cena
for i in range(30):
# Rotaciona quadrado
quadrado.rotate(i*DEGREES)
# Atualiza o quadro a cada 0.1 segundos
self.wait(0.1)7.2 Updaters
Em vez de criarmos animações no Manim desse jeito, uma opção melhor é usarmos updaters. São funções chamadas uma vez por frame renderizado. Criamos uma função chamada updater que tem como argumentos um Mobject mob e um dt que explicaremos depois. Dentro desta função, manipulamos o Mobject da forma que quisermos. Depois de criada, usamos o método add_updater e passamos a função updater que faz o resto do trabalho. Depois disso, usamos a função wait para especificar por quanto tempo queremos que dure a animação. Para parar a animação, usamos o remove_updaters ou clear_updaters.
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
# Criando variável de controle de rotação do quadrado
self.offset = 0
# Função updater usada para rotacionar o quadrado
def update_quadrado(mob, dt):
# Chamando método rotate do Mobject
mob.rotate(DEGREES)
# Criando quadrado
quadrado = Square()
# Adicionando updater ao quadrado
quadrado.add_updater(update_quadrado)
# Adicionando quadrado à cena
self.add(quadrado)
# Definindo 4 segundos de animação
self.wait(4)
# removendo updater do quadrado
quadrado.remove_updater(update_quadrado)
self.wait()Há algumas situações que não podemos atualizar alguma propriedade do objeto. Por exemplo, não podemos mudar os pontos de início e fim do objeto Line. Para isso, transformamos o objeto em outro Line utilizando o become dentro da função updater.
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
# Definindo variável de controle para a posição do fim da reta
self.offset = 0
# Definindo posição de fim
inicio = ORIGIN
# Criando círculo
circulo = Circle()
# Criando reta
linha = Line(start=inicio, end=circulo.point_from_proportion(0))
def update_linha(mob, dt):
# atualizando posição do ponto
self.offset += 0.5*dt
# Utilizando o become para atualizar a reta
mob.become(Line(inicio, circulo.point_from_proportion(self.offset % 1)))
self.add(linha, circulo)
linha.add_updater(update_linha)
self.wait(4)
self.remove_updater(update_linha)
self.wait()##Obs:
point_from_proportioné um método de Mobjects que aceita um número de 0 a 1 e retorna a posição proporcional ao número passado. Se o Mobject for um círculo e passamos 0.5 para o método, ele retornará o ponto do círculo à 180º.
7.3 mob e dt
Agora que vimos como utilizar os updaters, vamos entender o que os argumentos mob e dt são. O argumento mob é aquele que recebe o objeto que o updater está chamando. Por exemplo, se tivermos o seguinte código:
ponto = Dot()
def updater(mob, dt):
# código do updater
ponto.add_updater(updater)O objeto ponto será passado como mob para a função updater.
Mas e o dt? Ao chamar o método add_updater, a função passada como parâmetro será chamada a cada frame, ou seja, se o vídeo tiver mais quadros/frames por segundo (\(N_{\text{fps}}\)), a animação será mais rápida. Para que isso não aconteça, usamos o dt que possui valor \(\displaystyle \frac{1}{N_{\text{fps}}}\). Com isso, se renderizarmos em diferentes \(N_{\text{fps}}\), vamos obter o mesmo resultado quanto à velocidade da animação.
Por exemplo, uma animação com \(N_{\text{fps}}=15\) fps (frames por segundo) (opção -ql):
%%manim -ql -v WARNING Animacao
class Animacao(Scene):
def construct(self):
self.offset = 0
inicio = ORIGIN
circulo = Circle()
linha = Line(start=inicio, end=circulo.point_from_proportion(0))
def update_linha(mob, dt):
self.offset += 0.5*dt
mob.become(Line(inicio, circulo.point_from_proportion(self.offset % 1)))
self.add(linha, circulo)
linha.add_updater(update_linha)
self.wait(4)
self.remove_updater(update_linha)
self.wait()Agora uma animação com \(N_{\text{fps}}=60\) fps (opção -qh).
%%manim -qh -v WARNING Animacao
class Animacao(Scene):
def construct(self):
self.offset = 0
inicio = ORIGIN
circulo = Circle()
linha = Line(start=inicio, end=circulo.point_from_proportion(0))
def update_linha(mob, dt):
self.offset += 0.5*dt
mob.become(Line(inicio, circulo.point_from_proportion(self.offset % 1)))
self.add(linha, circulo)
linha.add_updater(update_linha)
self.wait(4)
self.remove_updater(update_linha)
self.wait()
- Produção de animações no Manim
Agora que vimos como utilizar o Manim com exemplos básicos, vamos ver um pouco como criar animações mais completas. Mas se prepare pois elas também darão muito mais trabalho!
##8.1 Roteiro e planejamento
No mundo da programação, programadores possuem a mania de querer começar a codificar antes de pensar no que eles precisam fazer. O mesmo vale aqui no Manim. Estamos escrevendo códigos para criar vídeos. É uma boa ideia planejar o que fazer antes de começar a programar. Para isso, é interessante criar um roteiro para a animação. Não precisa ser algo muito complexo ou bonito, mas que você entenda e que te ajude a criar as animações. É possível utilizar outros softwares para isso como:
- Notion,
- OneNote,
- ou até o bloco de notas
- ou colocar no próprio código
- ou até em uma folha de papel !
Pode ser em qualquer forma, contanto que você entenda e que te ajude.
##8.2 Editor de texto e ambiente de desenvolvimento
Como estamos usando código para produzir animações, apenas o bloco de notas não é o suficiente para produzir animações no Manim. É possível, mas nada eficiente. Para isso, existem as IDEs (Ambientes de Desenvolvimento Integrados). Eles são ferramentas que nos auxiliam a criar códigos. De certa forma, o Google Collab é uma IDE, mas com poucos recursos. Alguns dos recursos de IDEs que pdem ser citados são:
- Auto-complete: nos dá opção do que podemos digitar no código.
- Documentação: exibe a documentação de funções, classes e métodos ao passar o cursor por cima.
- Refatoração: nos permite trocar nomes de variáveis em vários pontos do código dependendo do contexto, procurar por nomes e trocá-los por outros.
- Build & Run: nos permite rodar o código sem ter que digitar pelo terminal.
- Terminal integrado: nos dá acesso à linha de comando sem sair do IDE.
Também podemos usar editores de texto que não possuem todas essas ferramentas, mas é possível instalar plugins que dão acesso a essas ferramentas. Algumas das IDEs e editores de texto são:
- Pycharm: IDE com inúmeras ferramentas para desenvolvimento
- Visual Studio Code: editor de texto leve que permite instalar extensões que dão ferramentas para desenvolvimento
8.3 Ambiente virtual
No Python, é interessante organizarmos as bibliotecas que usamos e não usar simplesmente instalá-las todas globalmente. Para isso, usamos a virtuale onde instalamos todas as bibliotecas necessárias.
- Comando para criar uma venv
python -m venv <nome da venv>- Comando para instalar o manim na venv
pip install manim8.4 Estrutura do projeto
A organização em um projeto é muito importante. Organizar arquivos em diferentes pastas, cada uma com arquivos em comum. Ao renderizar coisas no Manim, elas ficam armazenadas dentro da pasta media. Damos o nome da nossa animação, por exemplo, geometria_analitica e colocamos um arquivo .py e um textos.txt onde armazenamos os textos usados na animação. E temos o ambiente virtua visto no último tópico
Obs: Essa parte de textos é opcional, mas serve para organizarmos o processo de criação da animação.
Desse modo, teremos uma estrutura parecida com a seguinte:
- geometria_analitica
- anim.py
- textos.txt
- media
- venv
Com as coisas separadas, o projeto fica mais organizado.
##8.5 Uso de comentários
Agora que abordamos a organização do projeto em pastas, vamos abordar a organização do código. Para isso, usaremos os comentários. Como já vimos, existem 2 tipos de comentários, os de uma linha e o de múltiplas linhas. Ns exemplos de códgos anteriores, comentamos cada linha para explicar o que estava acontecendo no código, apenas para fins didáticos, entretanto, essa não é uma forma interessante de usar os comentários. Devemos usá-los para anotar coisas de um modo mais geral. Por exemplo, no código de updaters
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
# -------- Dados --------
self.offset = 0
inicio = ORIGIN
# -------- Mobjects --------
circulo = Circle()
linha = Line(start=inicio, end=circulo.point_from_proportion(0))
# -------- Updaters --------
def update_linha(mob, dt):
'''
Acompanha a reta ao redor do círculo
'''
self.offset += 0.5*dt
mob.become(Line(inicio, circulo.point_from_proportion(self.offset % 1)))
# -------- Animações --------
self.add(linha, circulo)
linha.add_updater(update_linha)
self.wait(4)
self.remove_updater(update_linha)
self.wait()Usamos os comentários para separar dados, Mobjects e animações, e para documentar as funções.
##8.6 Separando textos em outros arquivos
Ao criarmos textos no Manim, temos que dar nome a cada um deles. Para simplificar essa tarefa, podemos armazená-los em outro arquivo. É para isso que serve o textos.txt. Nele armazenamos os textos usados nas animações e quando precisarmos mudá-los, basta mudar no arquivo e ele mudará na animação. Podemos usar um código para pegar o conteúdo do arquivo e colocá-lo em uma lista onde estão todos os textos.
Criando o arquivo textos.txt:
with open('textos.txt', 'w') as arq:
arq.write('Arquivo de textos \nTexto 1 \nTexto 2 \nTextos 3') Exemplo de animação com o uso do arquivo:
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
textos = self.config_textos('textos.txt')
for texto in textos:
self.play(Write(texto))
self.play(FadeOut(texto))
# Função para pear os textos de um arquivo e transformá-los em Text
def config_textos(self, arq_nome):
# Abrindo arquivo
with open(arq_nome, 'r') as arq:
# Lendo linhas do arquivo e armazenando em lista
textos = arq.readlines()
m_textos = []
# Transformando a lista de texto em lista de Text
for texto in textos:
m_textos.append(Text(texto))
return m_textos8.7 Generalização de cenas
Para a organização do código, é interessante dividir as partes em diferentes funções. Algumas dessas funções contém apenas uma cena estática, mas outras, é possível generalizar essa função. Por exemplo, se tivermos uma função animando um gráfico, podemos generalizar a função que será utilizada no gráfico.
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
self.desenhar_reta(lambda x: x**2)
# Definindo função que pode pegar qualquer função e criar o gráfico a artir dela
def desenhar_reta(self, f):
eixos = Axes()
grafico = eixos.get_graph(f, (-2, 2))
self.play(Write(eixos))
self.play(Write(grafico))8.8 Simplificando funções
Num código usando o Manim, frequentemente precisamos usar diversas linhas de código com a mesma forma. Por exemplo, um código pode ter diversas linhas com self.play(Write()). Em vez de repetir essas linhas ao longo do código principal, podemos simplificar todo o código usando funções lambda.
%%manim -qm -v WARNING Animacao
class Animacao(Scene):
def construct(self):
w = lambda mob: self.play(Write(mob))
eixos = Axes()
grafico = eixos.get_graph(lambda x: x**2)
w(eixos)
w(grafico)8.9 Criando seus próprios objetos
Os objetos do Manim são utilizados apenas para serem renderizadas no vídeo. Por exemplo, dados de uma elipse como o semi-eixo menor e o semi-eixo maior não são armazenados nos objetos do Manim. Podemos criá-los e herdar da classe Ellipse.
%%manim -qm -v WARNING Animacao
# Classe que armazena objeto gráfico elipse e seus dados
class MinhaElipse(Ellipse):
def __init__(self, a, b):
self.a = a
self.b = b
# Definindo as propriedades da elipse se a > b
if self.a > self.b:
# Chamando construtor da classe pai
super().__init__(2*self.a, 2*self.b)
c = np.sqrt(self.a**2 - self.b**2)
self.f1, self.f2 = (-c, 0, 0), (c, 0, 0)
else:
# Chamando construtor da classe pai
super().__init__(self.b, self.a)
c = np.sqrt(2*self.b**2 - 2*self.a**2)
self.f1, self.f2 = (0, -c, 0), (0, c, 0)
class Animacao(Scene):
def construct(self):
# Instanciando objeto da classe MinhaElipse
e = MinhaElipse(3, 2)
focos = VGroup(Dot(e.f1), Dot(e.f2))
self.play(Write(e))
self.play(Write(focos))
- Finalizando com um exemplo prático
Chegamos ao fim deste pequeno manual sobre Manim/Python. Para o fim, deixaremos um exemplo de produção de uma animação. Primeiro, iremos apresentar a ideia da animação, ou seja, o que queremos mostrar com ela. Em seguida, iremos estruturar o projeto mostrando o roteiro com os passos a serem seguidos para se completar a animação e os objetos e os movimentos necessários. Por fim, apresentaremos o código do Manim que produz a animação.
Vamos supor que queremos animar o processo de se calcular o comprimento da diagonal de um quadrado de lado \(a\). Um possível roteiro com as etapas da animação está mostrado a seguir. Entre colchetes [ ] estão os principais Mobjects e animações necessárias em cada etapa.
A animação começaria com um quadrado aparecendo na tela. [
Square,FadeIn]Depois disso, o valor do lado (\(a\)) seria mostrado próximo a dois lados consecutivos do quadrado. [
MathTex,Write]Em seguida, a diagonal do quadrado apareceria na tela com uma cor diferente da do quadrado. [
Line,Write,set_color]Próximo a ela, apareceria então o texto \(x=?\). Esse texto vai indicar que queremos determinar o comprimento da diagonal. [
MathTex,Write]O passo seguinte seria destacar o triângulo formado por dois lados consecutivos do quadrado e a diagonal, indicando que é um triângulo retângulo (mostrando que o ângulo entre os lados é reto). O destaque seria feito desenhando o triângulo com outra cor. [
Polygon]Com a informação de que é um triângulo retângulo, seria feita a manipulação algébrica: \(x^2 = a^2 + a^2 \rightarrow x^2 = 2a^2 \rightarrow x = \sqrt{2a^2} \rightarrow x = \sqrt{2}a\). [
MathTex,TransformMatchingTex,ReplacementTransform]Após essa manipulação, a expressão \(x = \sqrt{2}a\) é movida para a região próxima à diagonal. [
MathTex,move_to]
Uma representação visual desse roteiro é apresentado na imagem a seguir (criada com o OneNote).

Definido o roteiro, primeiramente temos que pensar nos objetos que aparecem em mais de um passo. Isso porque vamos dividir os passos em funções no código. Como quase todos os objetos são utilizados por mais de um passo da cena, vamos defini-los todos como globais à cena, ou seja, usar o self em todos os objetos gráficos.
Vamos ao código. Primeiramente vamos definir o nome da cena, nomeando-a de DiagonalQuadrado. Também vamos declarar os métodos (funções de um objeto) dos passos da animação. Não precisa ser um método para cada passo, mas que tenhamos um certo número que deixe o código organizado. Também declaramos uma função para as figuras geométricas que aparecerão na cena. Com isso, teremos a seguinte estrutura do código:
class DiagonalQuadrado(Scene):
def construct(self):
# código da função
def config_global(self):
# código da função
def mostrar_quadrado(self):
# código da função
def mostrar_triangulos(self):
# código da função
def mostrar_manipulacao_algebrica(self):
# código da função
Agruparemos a definição e configuração dos objetos gráficos, textos, equações e funções auxiliares dentro da função config_global.
Quadrado:
self.quadrado = Square(side_length=tamanho_quadrado)\
.set_color(cor_quadrado)\
.move_to(posicao_quadrado)Triângulo:
cantos_triangulo = (
get_lados_quadrado(self.quadrado)[1],
get_lados_quadrado(self.quadrado)[2],
get_lados_quadrado(self.quadrado)[3],
)
self.triangulo = Polygon(*cantos_triangulo).set_color(cor_triangulo)Quadrado com um ponto no meio para representar o símbolo do ângulo reto do triângulo retângulo:
ponto_angulo_retangulo = get_lados_quadrado(self.quadrado)[2]\
+ 0.5*tamanho_angulo_retangulo*UP\
+ 0.5*tamanho_angulo_retangulo*RIGHT
self.angulo_retangulo = VGroup(
Square(side_length=tamanho_angulo_retangulo)\
.move_to(ponto_angulo_retangulo)
.set_color(cor_angulo_retangulo),
Dot(ponto_angulo_retangulo).scale(0.15*tamanho_quadrado)
)Diagonal do quadrado:
pontos_diagonal = (
get_lados_quadrado(self.quadrado)[1],
get_lados_quadrado(self.quadrado)[3]
)
self.diagonal = Line(*pontos_diagonal).set_color(cor_diagonal)Agora as cores, tamanhos e posições dos objetos.
cor_quadrado = WHITE
cor_lados_label = WHITE
cor_diagonal = RED
cor_x_label = cor_diagonal
cor_triangulo = PURPLE
cor_angulo_retangulo = BLUE
tamanho_quadrado = 4
tamanho_angulo_retangulo = tamanho_quadrado/10
posicao_equacoes = 3*RIGHT
posicao_quadrado = 2*LEFTDefinimos as variáveis de cor e posição para cada objeto para facilitar alterações caso necessário.
Textos e equações.
\(a\):
self.lados_label = VGroup(
MathTex('a').next_to(self.quadrado, direction=LEFT, buff=0.5),
MathTex('a').next_to(self.quadrado, direction=DOWN, buff=0.5)
).set_color(cor_lados_label)\(x\):
self.x_label = MathTex('x=', '?').next_to(self.quadrado, direction=RIGHT, buff=0.5).set_color(cor_x_label)Equações:
equacoes = [
MathTex('x^2', '=', 'a^2', '+', 'a^2'),
MathTex('x^2=2x^2'),
MathTex('x=\sqrt{2a^2}'),
MathTex('x=', '\sqrt{2}a')
]
self.equacoes = [
equacao.move_to(posicao_equacoes)
for equacao in equacoes
]Resultado:
self.resultado = MathTex('x=', '\sqrt{2}a')\
.move_to(self.triangulo.get_center() + 0.5*UP + 0.8*RIGHT)\
.set_color(cor_x_label)Função auxiliar para obter as coordenadas dos vértices do quadrado:
def get_lados_quadrado(quadrado):
lados_quadrado = [
quadrado.point_from_proportion(i)
for i in np.arange(0, 1.25, 0.25)
]
return lados_quadradoEssa função é usada também para obter informações para a construção do triângulo e do quadrado que representa o ângulo reto:
def get_lados_quadrado(quadrado):
lados_quadrado = [
quadrado.point_from_proportion(i)
for i in np.arange(0, 1.25, 0.25)
]
return lados_quadrado
cantos_triangulo = (
get_lados_quadrado(self.quadrado)[1],
get_lados_quadrado(self.quadrado)[2],
get_lados_quadrado(self.quadrado)[3],
)
ponto_angulo_retangulo = get_lados_quadrado(self.quadrado)[2]\
+ 0.5*tamanho_angulo_retangulo*UP\
+ 0.5*tamanho_angulo_retangulo*RIGHTAs funções que farão as animações dos objetos ficarão escritas como:
mostrar_quadrado()
def mostrar_quadrado(self):
write = lambda *mobs: self.play(*(Write(mob) for mob in mobs))
write(self.quadrado)
write(self.lados_label)
write(self.diagonal, self.x_label)mostrar_triangulo()
def mostrar_triangulo(self):
write = lambda *mobs: self.play(*(Write(mob) for mob in mobs))
fadeout = lambda *mobs: self.play(FadeOut(*mobs))
play = lambda *anim: self.play(*anim)
write(self.triangulo)
fadeout(self.quadrado)
play(self.x_label.animate.move_to(self.triangulo.get_center() + 0.5*UP + 0.5*RIGHT))
write(self.angulo_retangulo)mostrar_manipulacao_algebrica()
def mostrar_manipulacao_algebrica(self):
wait = lambda t=1: self.wait(t)
play = lambda *anim, t=1: self.play(*anim, run_time=t)
fadein = lambda *mobs: self.play(FadeIn(*mobs))
play(
ReplacementTransform(self.x_label.copy(), self.equacoes[0][0]),
ReplacementTransform(self.lados_label[0].copy(), self.equacoes[0][2]),
ReplacementTransform(self.lados_label[1].copy(), self.equacoes[0][4]),
t=3
)
fadein(self.equacoes[0][1], self.equacoes[0][3])
wait()
play(TransformMatchingTex(self.equacoes[0], self.equacoes[1]), t=3)
wait()
play(TransformMatchingTex(self.equacoes[1], self.equacoes[2]), t=3)
wait()
play(TransformMatchingTex(self.equacoes[2], self.equacoes[3]), t=3)
wait()
play(
TransformMatchingTex(self.x_label, self.resultado),
ReplacementTransform(self.equacoes[3][1].copy(), self.resultado[1])
)
wait()Agrupando tudo isso, teremos um possível código para produzir a animação desejada:
%%manim -qm -v WARNING DiagonalQuadrado
class DiagonalQuadrado(Scene):
def construct(self):
self.config_global()
self.mostrar_quadrado()
self.mostrar_triangulo()
self.mostrar_manipulacao_algebrica()
# função com configurações globais da cena
def config_global(self):
# função auxiliar para obter a posição dos vértices do quadrado
def get_lados_quadrado(quadrado):
lados_quadrado = [
quadrado.point_from_proportion(i)
for i in np.arange(0, 1.25, 0.25)
]
return lados_quadrado
# definição das cores dos objetos
cor_quadrado = WHITE
cor_lados_label = WHITE
cor_diagonal = RED
cor_x_label = cor_diagonal
cor_triangulo = PURPLE
cor_angulo_retangulo = BLUE
# definição do tamanho dos objetos
tamanho_quadrado = 4
tamanho_angulo_retangulo = tamanho_quadrado/10
# posições dos objetos
posicao_equacoes = 3*RIGHT
posicao_quadrado = 2*LEFT
# cria o quadrado
self.quadrado = Square(side_length=tamanho_quadrado)\
.set_color(cor_quadrado)\
.move_to(posicao_quadrado)
self.lados_label = VGroup(
MathTex('a').next_to(self.quadrado, direction=LEFT, buff=0.5),
MathTex('a').next_to(self.quadrado, direction=DOWN, buff=0.5)
).set_color(cor_lados_label)
# localiza os pontos da diagonal
pontos_diagonal = (
get_lados_quadrado(self.quadrado)[1],
get_lados_quadrado(self.quadrado)[3]
)
# cria segmento de reta que representa a diagonal
self.diagonal = Line(*pontos_diagonal).set_color(cor_diagonal)
# texto para representar a diagonal como incógnita
self.x_label = MathTex('x=', '?').next_to(self.quadrado, direction=RIGHT, buff=0.5).set_color(cor_x_label)
# obtém os vértices do quadrado com os quais será desenhado o triângulo
cantos_triangulo = (
get_lados_quadrado(self.quadrado)[1],
get_lados_quadrado(self.quadrado)[2],
get_lados_quadrado(self.quadrado)[3],
)
# cria o triângulo
self.triangulo = Polygon(*cantos_triangulo).set_color(cor_triangulo)
# determina a posição onde será colocado um ponto para representar o
# ângulo reto
ponto_angulo_retangulo = get_lados_quadrado(self.quadrado)[2]\
+ 0.5*tamanho_angulo_retangulo*UP\
+ 0.5*tamanho_angulo_retangulo*RIGHT
# cria um quadrado com um ponto no centro
self.angulo_retangulo = VGroup(
Square(side_length=tamanho_angulo_retangulo)\
.move_to(ponto_angulo_retangulo)
.set_color(cor_angulo_retangulo),
Dot(ponto_angulo_retangulo).scale(0.15*tamanho_quadrado)
)
# define as equações a serem usadas
equacoes = [
MathTex('x^2', '=', 'a^2', '+', 'a^2'),
MathTex('x^2=2x^2'),
MathTex('x=\sqrt{2a^2}'),
MathTex('x=', '\sqrt{2}a')
]
# cria as equações e coloca-as nas posições corretas
self.equacoes = [
equacao.move_to(posicao_equacoes)
for equacao in equacoes
]
# cria a equação que representa o resultado final
self.resultado = MathTex('x=', '\sqrt{2}a')\
.move_to(self.triangulo.get_center() + 0.5*UP + 0.8*RIGHT)\
.set_color(cor_x_label)
#####################
# início da animação
#####################
def mostrar_quadrado(self):
write = lambda *mobs: self.play(*(Write(mob) for mob in mobs))
# Faz aparecer o quadrado na tela (etapa (1))
write(self.quadrado)
# Faz aparecer o nome para o lado do quadrado (etapa (2))
write(self.lados_label)
# Faz aparecer a diagonal do quadrado e o valor da diagonal como incógnita
# (etapa (3) e (4))
write(self.diagonal, self.x_label)
def mostrar_triangulo(self):
write = lambda *mobs: self.play(*(Write(mob) for mob in mobs))
fadeout = lambda *mobs: self.play(FadeOut(*mobs))
play = lambda *anim: self.play(*anim)
# Destaca triângulo e indica que ele é retângulo (etapa (5))
write(self.triangulo)
fadeout(self.quadrado)
play(self.x_label.animate.move_to(self.triangulo.get_center() + 0.5*UP + 0.5*RIGHT))
write(self.angulo_retangulo)
def mostrar_manipulacao_algebrica(self):
wait = lambda t=1: self.wait(t)
play = lambda *anim, t=1: self.play(*anim, run_time=t)
fadein = lambda *mobs: self.play(FadeIn(*mobs))
# Animação das manipulações algébricas
# etapa (6)
play(
ReplacementTransform(self.x_label.copy(), self.equacoes[0][0]),
ReplacementTransform(self.lados_label[0].copy(), self.equacoes[0][2]),
ReplacementTransform(self.lados_label[1].copy(), self.equacoes[0][4]),
t=3
)
fadein(self.equacoes[0][1], self.equacoes[0][3])
wait()
play(TransformMatchingTex(self.equacoes[0], self.equacoes[1]), t=3)
wait()
play(TransformMatchingTex(self.equacoes[1], self.equacoes[2]), t=3)
wait()
play(TransformMatchingTex(self.equacoes[2], self.equacoes[3]), t=3)
wait()
# etapa (7)
play(
TransformMatchingTex(self.x_label, self.resultado),
ReplacementTransform(self.equacoes[3][1].copy(), self.resultado[1])
)
wait()
#####################
# fim da animação
#####################
- Consultando documentação
O Manim possui uma comunidade muito ativa atualmente que mantém o projeto e sua documentação. Para acessar essa documentação e redes sociais, acesse o seguinte link. Nele estão todas as formas de comunicação com a comunidade. Grande parte dos exemplos de animação criados neste manual foram criados consultando essa documentação. Além da documentação oficial, há também outras fontes que podem ser consultadas. Uma delas é o canal de Alexander Vázquez Theorem of Beethoven e os materiais produzidos por ele disponível no Github.