Pêndulos acoplados

Autor

Vitor Coluci

Oscilações estão por toda a parte. Estão numa molécula que vibra, numa criança brincando num balanço, nos elétrons que se movimentam dentro do seu celular. A molécula, a criança e o elétron são exemplos de osciladores. Um outro exemplo de oscilador muito conhecido dos físicos é o pêndulo: um corpo preso a uma corda que é posto a oscilar.

Muitas vezes, não temos apenas um oscilador oscilando no sistema. Temos vários, como a montagem mostrada na figura acima. Na montagem, temos dois pêndulos que podem oscilar. Além disso, as oscilações não são independentes, elas são acopladas. O acoplamento é produzido, neste caso, pela barra horizontal.

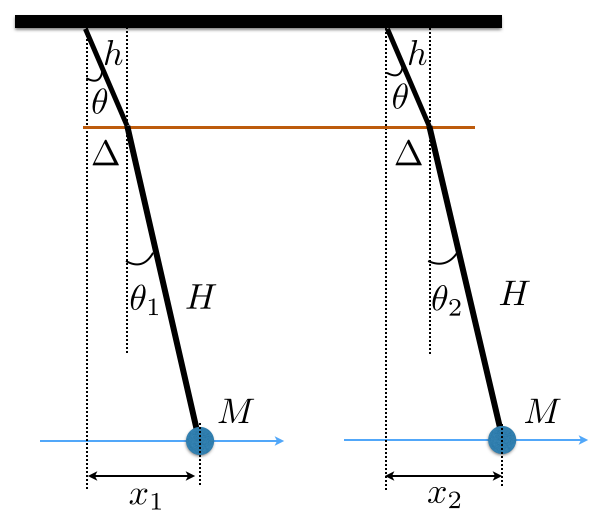
Faremos aqui uma análise do movimento de pêndulos acoplados. Para isso, usaremos um modelo para representar a montagem acima. O modelo é o da figura a seguir, onde tanto as cordas como a barra de acoplamento serão consideradas de massa desprezível quando comparadas a massa dos pêndulos (porcas, neste caso). Os comprimentos e ângulos relevantes para descrevermos o movimento estão indicados na figura. Localizaremos o pêndulo da esquerda pela variável $x_1$ e o da direita pela variável $x_2$, ambas medidas a partir do ponto onde os pêndulos estão em suas posições de equilíbrio.

O movimento de um único pêndulo para pequenas oscilações (neste caso, conhecido como pêndulo simples) é descrito pela equação diferencial

\[ \ddot{x} = -\frac{g}{H}x \]

onde $g$ é a aceleração da gravidade, $H$ é o comprimento do pêndulo e $\displaystyle \ddot{x}\equiv \frac{d^2x}{dt^2}$. Essa equação é obtida a partir das forças que agem sobre o pêndulo.

Para o sistema com dois pêndulos, teremos o seguinte conjunto de 2 equações:

\[\displaystyle \left\{ \begin{array}{ccc} \ddot{x}_1 & = &\displaystyle -\frac{g}{H}(x_1 - \Delta(x_1,x_2) ) \\ \ddot{x} _2 & = &\displaystyle -\frac{g}{H}(x_2 - \Delta(x_1,x_2) ) \\ \end{array} \right. .\] onde $\Delta(x_1,x_2)$ depende de $x_1$ e $x_2$ e representa matematicamente o acoplamento entre os pêndulos. As soluções das equações, isto é, $x_1(t)$ e $x_2(t)$ fornecerão o movimento de cada pêndulo. As duas equações acima são acopladas pois a solução da primeira é usada para construir a segunda e vice-versa. Portanto, vamos primeiramente desacoplá-las!

Para isso, vamos primeiramente subtrair uma equação da outra. Isso resulta em

\[ \displaystyle \ddot{x_1}-\ddot{x_2} = -\frac{g}{H}(x_1-x_2)\]

Se agora definirmos $X_a\equiv x_1-x_2$, a equação acima pode ser reescrita como

\[ \displaystyle \ddot{X_a} = -\frac{g}{H}X_a\]

que é a oscilação de um pêndulo simples com frequência angular $\displaystyle \omega_a=\sqrt{\frac{g}{H}}$.

Vamos tentar agora somar as equações. Isso resulta em

\[ \displaystyle \ddot{x_1}+\ddot{x_2} = -\frac{g}{H}(x_1+x_2-2\Delta).\]

Como estamos considerando pequenas amplitudes (pêndulo simples), podemos ainda considerar que $\theta_1 \approx \theta_2 \approx \theta$, assim

\[ \displaystyle \frac{x_1}{H} \approx \frac{x_2}{H} \approx \frac{\Delta}{h}\]

\[ \displaystyle \frac{x_{1,2}-\Delta}{H} \approx \frac{x_{1,2}}{H+h} \]

e assim

\[ \displaystyle \ddot{x_1}+\ddot{x_2} = -\frac{g}{H+h}(x_1+x_2).\]

Definindo agora $X_b\equiv x_1+x_2$, a equação acima pode ser reescrita como

\[ \displaystyle \ddot{X_b} = -\frac{g}{H+h}X_b\]

que é a oscilação de um pêndulo simples com frequência angular $\displaystyle \omega_b=\sqrt{\frac{g}{H+h}}$, onde $\omega_a>\omega_b$.

As equações para $X_a$ e $X_b$ são desacopladas e tem soluções da forma

\[ \displaystyle X_a = A\cos(\omega_a t+\delta_a)\]

\[ \displaystyle X_b = B\cos(\omega_b t+\delta_b),\]

onde $A$, $B$, $\delta_a$ e $\delta_b$ são constantes de integração que dependem das condições iniciais, isto é, de que posição e velocidade os pêndulos tem em $t=0$.

Vamos considerar dois casos especiais das soluções acima.

$A=0\rightarrow X_a=x_1-x_2=0$ ou ainda $x_1=x_2=(B/2)\cos(\omega_b+\delta_b)$. Ou seja, os dois pêndulos oscilam com a mesma frequência $\omega_b$ e com a mesma amplitute $B/2$. Eles oscilam em fase. Este movimento, onde os osciladores tem a mesma frequência, é chamado de modo normal de oscilação. $B=0\rightarrow X_b=x_1+x_2=0$ ou ainda $x_1=-x_2=-(A/2)\cos(\omega_a+\delta_a)$. Ou seja, os dois pêndulos oscilam com a mesma frequência $\omega_a$ mas agora com amplitudes opostas! Os dois pêndulos se aproximam e se afastam juntos. Este movimento é um outro modo normal de oscilação.

Para um caso geral, diferente dos dois apresentados acima, a solução será uma combinaçcão linear dos dois modos normais de oscilação. Por exemplo, se largarmos cada pêndulo a partir de ângulos diferentes ( $\theta_1(0)\neq\theta_2(0)$ ), o movimento dos dois pêndulos envolverá ambos os modos normais, parecendo um movimento caótico.

Vamos analisar o caso onde $x_1=X_0$, $x_2=0$ e $\dot{x}_1=\dot{x}_2=0$ (ou $X_a=X_0$, $X_b=X_0$ e $\dot{X}_a=\dot{X}_b=0$ ). Para este caso, a solução do sistema de equações diferenciais acopladas é:

\[ \displaystyle x_1(t) =X_0 \cos \left( \frac{\omega_a-\omega_b}{2}t\right)\cos \left( \frac{\omega_a+\omega_b}{2}t\right) \]

\[ \displaystyle x_2(t) =X_0 \sin \left( \frac{\omega_a-\omega_b}{2}t\right)\sin \left( \frac{\omega_a+\omega_b}{2}t\right) \]

Os termos envolvendo $ _a-_b $ modulam a amplitude dos movimentos e correspondem ao que chamamos de batimento. A frequência de batimento $f$ será portanto

\[\displaystyle f = \frac{\omega_a-\omega_b}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{gh}{H(H+h)}}\]

e o período de batimento $T=1/f$,

\[\displaystyle T = 2\pi\sqrt{\frac{H(H+h)}{gh}}.\]

O caso sem acoplamente ocorre quando $h=0$ onde o movimento de um dos pêndulos não influencia o movimento do outro.

Use a animação a seguir (Autor Vitor Coluci) para ver como será o movimento dos pêndulos para diferentes valores de $h$, a localização da barra de acoplamento. Notem que após um tempo de $T/2$ de iniciado o movimento do pêndulo 1, toda a energia dele é transferida para o pêndulo 2 (a amplitude do pêndulo 1 é zero enquanto a do pêndulo 2 é máxima).

Para os curiosos

A montagem dos pêndulos acoplados por uma barra foi proposta originalmente por Priest e Poth em 1982 no trabalho Teaching Physics with coupled pendulums. A motivação deles foi um evento ocorrido durante um musical na escola onde trabalhavam!

Uma montagem semelhante àquela que estudamos aqui por ser vista no trabalho de Young-Ki Cho Teaching the Physics of a String-Coupled Pendulum Oscillator: Not Just for Seniors Anymore (2012).

Você sabia que pêndulos acoplados tem uma conexão com a física das partículas elementares? Pois é, veja neste vídeo (em inglês) de Martin Archer esta conexão !

Deixamos aqui uma pergunta: O que acontecerá com o movimento dos dois pêndulos se eles tiverem comprimentos diferentes ? Que tal construir esta configuração ?

Ficou curioso sobre a dependência de $\Delta$ com $x_1$ e $x_2$ ? Aqui calculamos essa dependência usando a formulação Lagrangiana. Confira!