Ciclóide e a pista de skate

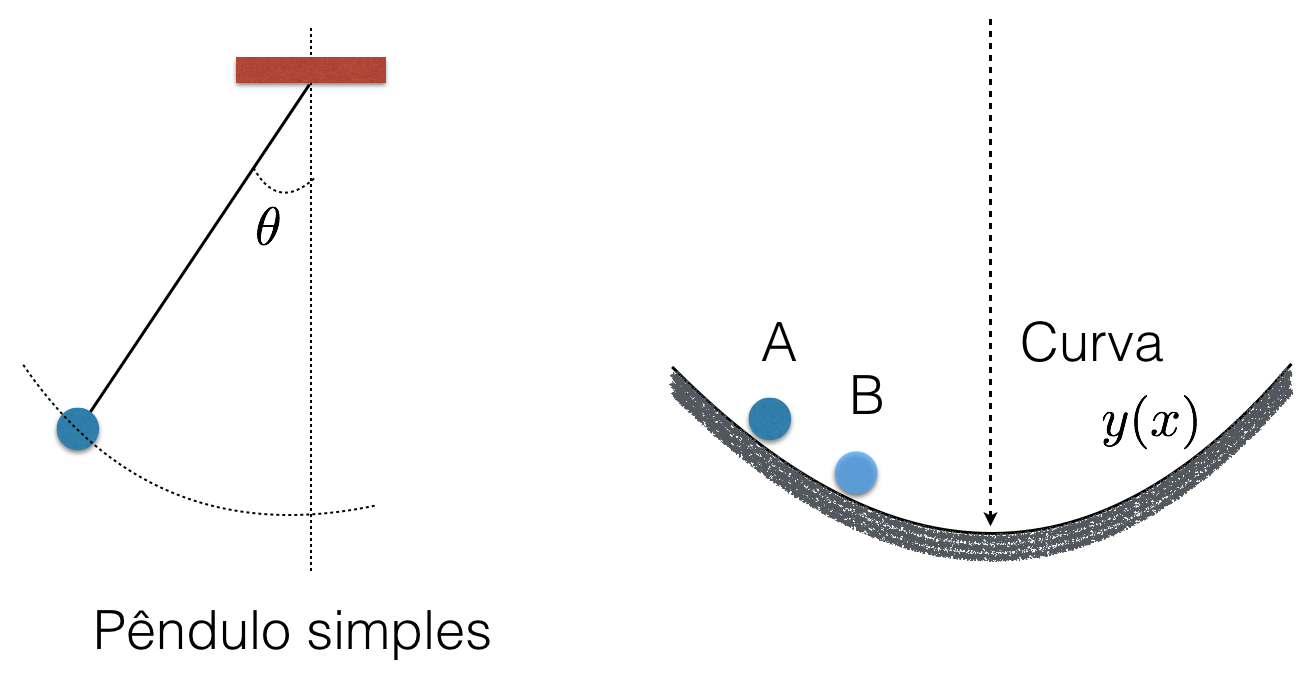
Num pêndulo simples, quando o ângulo é muito pequeno (\(\theta << 1\)), o período de oscilação independe do ângulo que largamos o corpo. O caminho descrito pelo corpo, ou seja, sua trajetória, segue uma curva \(y(x)\). No caso do pêndulo simples, essa curva é um trecho da circunferência, ou seja, \(x^2+y^2=L^2\), onde \(L\) é o comprimento do fio. Se largamos o corpo de um ângulo não tão pequeno (> 10\(^o\), por exemplo), o período de oscilação começa a depender do valor deste ângulo (veja a seção para curiosos aqui). Mesmo nestes casos, a trajetória continuaria sendo descrita por uma circunferência.

Será que existe uma curva que levaria um corpo a se movimentar de tal modo que o período de oscilação fosse independente do ângulo ou, em outras palavras, da posição que ele é largado a oscilar ? Isso seria equivalente a dizer que largarmos o corpo da posição A, mostrado na figura a seguir, ele chegaria até a parte mais baixa da curva (representada pela seta) no mesmo tempo que se largarmos o corpo da posição B. Lembre-se que estamos considerando, assim como fizemos para o pêndulos simples, a ausência de qualquer tipo de atrito.

A resposta a essa pergunta é SIM. 

Aqui estamos interessados em descobrir a curva que nos fornence determinadas propriedades, isto é, soluções para problemas que não são números, mas sim funções que são soluções para determinadas aplicações. 

Esse tipo de problema foi proposto por Christiaan Huygens em uma de suas cartas escritas para Gottfried W. Leibniz em 1670, e ficou conhecido como o problema da Tautócrona (tautó(mesmo) + chrónos (tempo) = tautóchrone (mesmo tempo) ). A resolução deste problema, feita pelo próprio Huygens, permitiu a construção do primeiro relógio preciso feito de pêndulo.

Vamos investigar então que curva é essa!

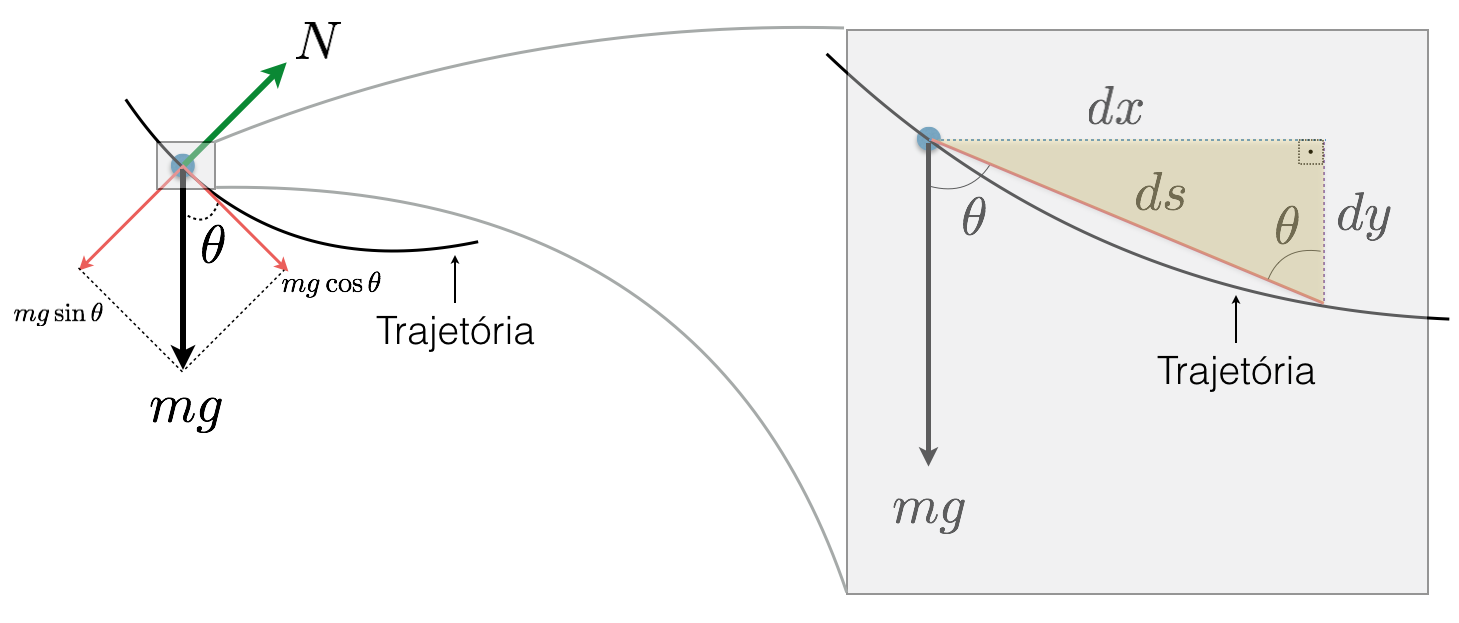
Quando o corpo está sobre a curva, ele está sob a ação da força peso (de valor \(mg\)) e da força normal (\(N\)). A componente da força peso que empurra o corpo ao longo da trajetória depende de onde ele está localizado na curva. E esta componente tem valor \(mg\cos\theta\) onde \(\theta\) é o ângulo que a reta tangente a trajetória faz com a direção vertical.

Como estamos desprezando qualquer forma de atrito, então a força resultante sobre o corpo na direção da trajetória é \(F=mg\cos\theta\). Analisando o movimento do corpo num curto intervalo de tempo onde o corpo se movimenta ao longo de um pequeno trecho \(ds\) da curva, podemos reescrever \(\cos\theta = dy/ds\), como ilustrado na figura a seguir.

Assim, a força resultante fica

\[\displaystyle F=mg\frac{dy}{ds}.\]

Como queremos que o período de oscilação seja independente de onde largamos o corpo, vamos impor que a equação acima seja da mesma forma que a equação de um oscilador harmônio (força resultante proporcional ao deslocamento), o qual também possui essa propriedade do período. Assim,

\[\displaystyle mg \frac{dy}{ds}=ks.\]

Essa equação é então integrada fazendo

\[\displaystyle mg \int dy = k \int s ds\]

o que resulta em

\[\displaystyle mgy=\frac{1}{2}ks^2 +\text{constante}\]

Essa equação nos dá a relação entre a coordenada \(y\) do corpo como sua posição ao longo da trajetória, medida por \(s\). Como, quando estamos na parte mais baixa da curva, \(y=0\), o valor de \(s\) deve ser zero, então o valor da constante acima deve ser também zero. Logo, podemos reescrever a equação acima, deixando \(s\) em função de \(y\) como

\[\displaystyle s=\sqrt{\frac{2mgy}{k}}.\]

Analisando o triângulo retângulo indicado na figura acima, vemos que vale a seguinte igualdade

\[\displaystyle (ds)^2=(dx)^2+(dy)^2\rightarrow \left(\frac{ds}{dy}\right)^2=1+\left(\frac{dx}{dy}\right)^2\]

Calculando \(ds/dy\) podemos substitui-lo na equação acima de forma que

\[\displaystyle 1+\left(\frac{dx}{dy}\right)^2 =\frac{g}{2\omega^2 y}\rightarrow \displaystyle dx=\sqrt{\frac{g}{2\omega^2 y}-1}dy\]

onde \(\omega^2\equiv k/m\).

A equação fornece a relação complicada entre \(y\) e \(x\) da curva. Para acharmos uma forma melhor de enxergarmos a curva, vamos fazer uma mudança de variáveis para eliminarmos a raiz quadrada que aparece na relação.

Se usarmos \(\displaystyle y=\frac{g}{4\omega^2}(1-\cos\phi)\) (de tal forma que \(y=0\) quando \(\phi=0\)) teremos que 

\[\displaystyle dy=\frac{g}{4\omega^2}\sin\phi d\phi\]

e

\[\displaystyle \sqrt{\frac{g}{2\omega^2 y}-1}=\sqrt{\frac{2}{1-\cos\phi}-1}=\sqrt{\frac{1+\cos\phi}{1-\cos\phi}}\rightarrow\]

\[\displaystyle \sqrt{\frac{1+\cos\phi}{1-\cos\phi}}= \sqrt{\frac{(1+\cos\phi)}{(1-\cos\phi)}\frac{(1+\cos\phi)}{(1+\cos\phi)}}= \sqrt{\frac{(1+\cos\phi)^2}{\sin^2\phi}}=\frac{1+\cos\phi}{\sin\phi}.\]

Assim,

\[\displaystyle dx=\sqrt{\frac{g}{2\omega^2 y}-1}dy=\frac{g}{4\omega^2}(1+\cos\phi)d\phi\]

que integrada nos leva à

\[\displaystyle \int dx=\frac{g}{4\omega^2}\int (1+\cos\phi)d\phi\]

\[\displaystyle x=\frac{g}{4\omega^2}(\phi+\sin\phi)+\text{constante}.\]

Considerando também que \(x=0\) quando \(\phi=0\), o valor da constante acima deve ser zero e, assim, finalmente chegamos à

\[\displaystyle x(\phi)=\frac{g}{4\omega^2}(\phi+\sin\phi)\]

\[\displaystyle y(\phi)=\frac{g}{4\omega^2}(1-\cos\phi)\]

que são as equações paramétricas que descrevem a curva que estávamos procurando. A animação a seguir mostra como é a forma desta curva. Ao variamos o valor de \(\phi\) obtemos um ponto (\(x,y\)) da curva. Essa curva se chama ciclóide.

O vídeo a seguir mostra, na prática, o processo de construção da ciclóide e o seu tautocronismo. 

Para os curiosos

A ciclóide também tem a propriedade de que, comparada com todas as outras curvas, um corpo deslizando por ela sob a ação da gravidade leva o menor tempo para chegar ao ponto mais baixo. Ou seja, a ciclóide tem a propriedade de ser braquistócrona ( do grego brakhisto (rápido) e chronos (tempo)). A animação a seguir mostra que um corpo, que percorre a ciclóide, chega antes na parte inferior do que se ele percorresse uma trajetória retilínea.

Para saber um pouco mais sobre a braquistócrona, veja o trabalho de Ana Luísa Sader Tagliolatto disponível aqui. Nele você poderá ver como a braquistócrona se relaciona com o cálculo variacional de Euler-Lagrange, com a lei de Snell, com o salvamento numa praia e com uma pista de skate.

Quer saber como se comporta a velocidade e a aceleração de um corpo que percorre uma braquistócrona ou ainda quanto tempo leva o corpo para descê-la, veja o artigo “Uma abordagem geométrica ao problema da braquistócrona” de M.A. De Andrade e L.G. Ferreira Filho.

O vídeo a seguir mostra um pouco mais sobre a história curiosa da braquistócrona, que envolveu disputas entre grandes matemáticos.